Anatomy of High-Performance Matrix Multiplication

http://www.cs.utexas.edu/~flame/pubs/GotoTOMS_revision.pdf

1. INTRODUCTION

实现接近最优性能的矩阵乘法，不仅需要在宏观层级了解如何将运算拆分成kernel，还需要在微观层级工程实现高性能kernel。这篇paper主要针对宏观问题，也就是如何发现高性能kernel，而不是微观层级的如何设计和实现高性能kernel。在一个复杂的多级内存架构下，¹方法优化减少在相邻层内存之间的数据搬移，与²³不同的是，¹提出“inner-kernel”概念，对于某些$m_c\times k_c$的矩阵$\tilde{A}$计算$C:=\tilde{A}B+C$，矩阵$\tilde{A}$以某种打包的格式连续存储，并且可以容纳在cache内。但是这里用到的内存结构是不现实的：

假设矩阵$\tilde{A}$的inner-kernel计算都在L1 cache
忽视了Translation Look-aside Buffer (TLB)问题最近的[^4]]观察到
浮点运算单元能够执行的浮点运算操作数，可以从寄存器流出到L2 cache的浮点数很少。
矩阵$\tilde{A}$尺寸的限制因素是TLB能访问的数据量

我们同时发现

我们考虑高性能矩阵乘法时需要考虑6种inner-kernel，¹[^5]只考虑了其中3种

第二章介绍了本文用到的符号，第三章介绍了一种分层的矩阵乘法实现方法，第四章介绍inner-kernel实现。第五章介绍了现实中最常见场景下的算法。第六章给出了现实中如何调整算法参数以优化性能。第七章介绍了不同架构下的算法性能。最后一章包含一些总结。

2. NOTATION

矩阵分解矩阵乘法的是核心，给定一个$m\times n$的矩阵$X$，本文中只考虑按行分块或者按列分块 $X= \begin{pmatrix} X_0 & X_1 & \cdots & X_{N-1} \end{pmatrix} = \begin{pmatrix} \check{X}_0 \\ \check{X}_1 \\ \cdots \\ \check{X}_{M-1} \\ \end{pmatrix}$ 这里除了$X_{N-1}$和$\check{X}{M-1}$以外，$X_j$都有$n_b$列，$\check{X}_i$都有$m_b$行，$X{N-1}$和$\check{X}_{M-1}$的行列可能会更少。原始矩阵的乘法将被分解成若干子矩阵的乘法，将三种常见的特殊尺寸的矩阵抽象出来

Fig3

Fig2

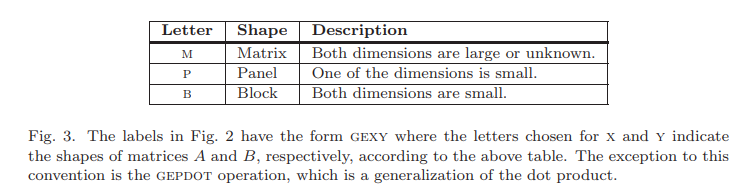
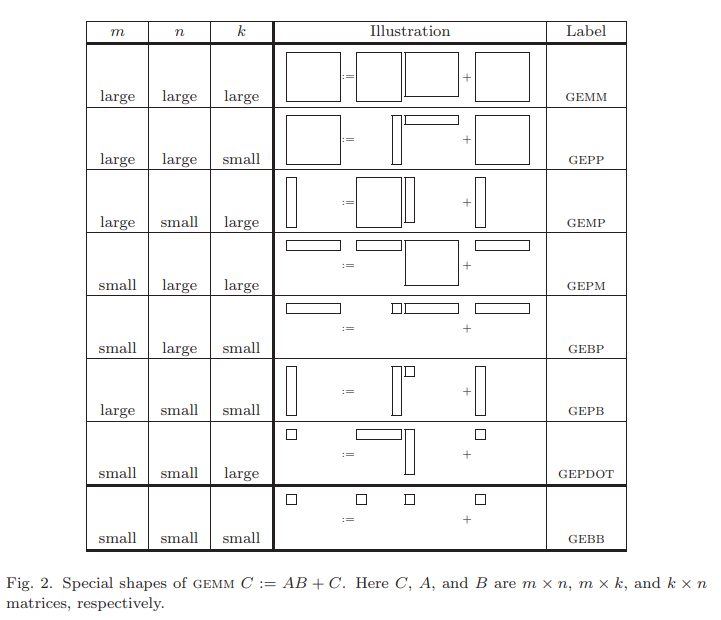
3. A LAYERED APPROACH TO GEMM

如下图所示，GEMM可以被分解成多个GEPP，GEMP或者GEPM，进一步可以分解成多个GEBP，GEPB或者GEDOT kernel。 Fig5

4. HIGH-PERFORMANCE GEBP, GEPB, AND GEPDOT

现在我们讨论GEBP，GEPB和GEDOT的高性能实现。首先我们在一个简单内存结构模型下分析数据搬移开销。更复杂和实际的内存结构模型将在4.2章节讨论。

4.1 Basics

下图左边是一个非常简单的多层内存模型，只有寄存器/ cache/RAM。 Fig6

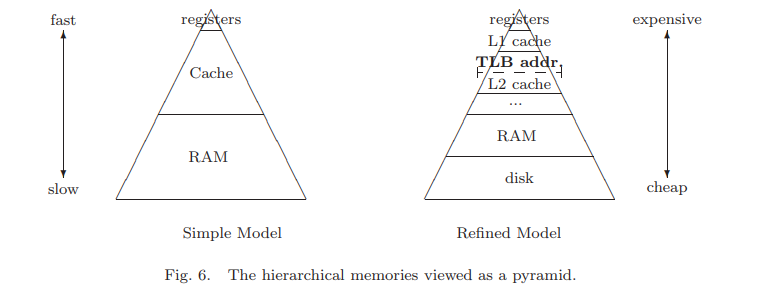
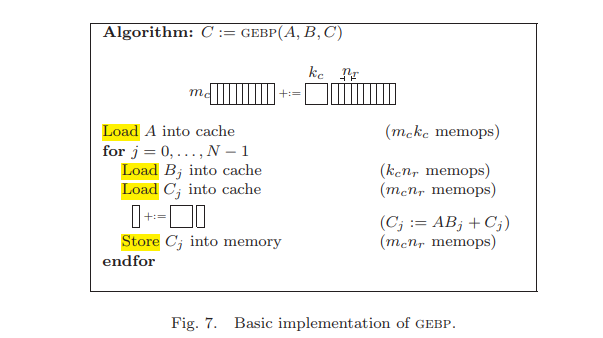
在这种简单模型结构下考虑优化GEBP，$C_{m_c,n}+=A_{m_c,k_c}B_{k_c,n}$，其中

$A$是block，$A\in \Bbb{R}^{m_c\times k_c}$
$B$是panel，$B\in \Bbb{R}^{k_c\times n}$
$C$也是panel，$C\in \Bbb{R}^{m_c\times n}$

Fig7

3个假设

Assumptions (a)：$m_c$和$k_c$都足够小，使得cache能够容纳矩阵$A$，矩阵$B$的$n_r$列$B_j$和矩阵$C$的$n_r$列$C_j$
Assumptions (b)：如果$A$，$B_j$和$C_j$都在cache里，那么$C_j:=AB_j+C_j$能全速利用CPU
Assumptions (c)：$A$ 可以一直保留在cache里不被切换出去

基于以上三点假设，上图中GEBP的RAM和cache之间的数据搬移开销为$m_ck_c+k_cn+2m_cn$ memops

把$A$从RAM加载到cache，$m_ck_c$
把$B_j$从RAM加载到cache，$k_cn$
把$C_j$从RAM加载到cache，$m_cn$
计算完，把$C_j$结果从cache加载到RAM，$m_cn$

而$C_j:=AB_j+C_j$的计算量为$2m_ck_cn$ flops，那么计算量和数据搬移的比例是 $\frac{2m_ck_cn}{m_ck_c+k_cn+2m_cn} \approx \frac{2m_ck_cn}{k_cn+2m_cn}=\frac{2m_ck_c}{k_c+2m_c}\frac{flops}{memops} \quad \text{where}\quad m_c<<n$

问题变成，如何选择矩阵$A$的尺寸$m_c$和$k_c$，使得矩阵尺寸满足Assumptions (a)-(c)，而且$\frac{2m_ck_c}{k_c+2m_c}$值最大。

最大化$k_cm_c$，尽可能选择最大尺寸的矩阵$A$，使得$A, B_j, C_j$能够放进cache
在$m_ck_c \leq K$前提下，求$\frac{2m_ck_c}{k_c+m_c}$最大值问题，数学上转换成几何问题，一个长方形边长分别是$2m_c$和$k_c$，在长方形面积受限$m_ck_c \leq K$条件下，如何最大化长方形周长$2(k_c+2m_c)$，这个问题在数学上的最优解就是$k_c=2m_c$，不应该是方阵?

现实中$k_c$的选择还受一些其他因素制约，我们将在6.3章节看到。类似地可以分析GEPB和GEDOT操作。

考虑更加实际的应用场景，假设矩阵是column-major order按列存储的。

4.2.1 Choosing the cache layer

Fig.6的右边描述了更准确的内存结构，实际上cache也是分成多层的。首先问题是，尺寸为$k_c\times m_c$的矩阵$A$应该保留在哪一层cache？答案肯定是，在满足Assumptions (a)-(c)的前提下，越快越好，最接近寄存器最快的那一层cache，也就是L1 cache。但是L1 cache天然地非常小，那么可以把矩阵$A$应该保留在L2 cache里，同时让尺寸$k_c\times m_c$更大一些? $R_{comp}$表示CPU能处理的浮点运算操作速度，$R_{load}$表示CPU能从L2 cache加载到寄存器的速度，假设

矩阵$A$保留在L2 cache，而矩阵$B_j$和$C_j$保留在L1 cache
L1 cache和寄存器之间带宽足够，也就是忽略矩阵$B_j$和$C_j$的加载时间

那么$C_j:=AB_j+C_j$的计算量为$2m_ck_cn_r$ flops，时间开销为$\frac{2m_ck_cn_r}{R_{comp}}$，带宽开销为从L2 cache加载矩阵$A$到寄存器的数据量$m_ck_c$，时间开销为$\frac{m_ck_c}{R_{loa d}}$。为了克服矩阵$A$的加载时间，必须保证 $\frac{2m_ck_cn_r}{R_{comp}} \geq \frac{m_ck_c}{R_{load}} \\ n_r \geq \frac{R_{comp}}{2R_{load}}$

$B_j$和$C_j$保留在L1 cache，$A$保留在L2 cache，希望矩阵计算时间大于L2 cache的加载时间，panel矩阵$B, C$按$n_r$行或$n_r$列拆分成$B_j, C_j$矩阵时，拆分尺寸$n_r$必须足够大，$n_r$的最小值与CPU浮点运算操作速度$R_{comp}$和L2 cache加载到寄存器的速度$R_{load}$相关。

4.2.2 TLB considerations

第二个考量与系统页管理有关。通常我们的系统使用虚拟内存，因此可用内存大小不受实际物理内存大小限制，内存是分页的。有一张page table来映射虚拟地址和物理地址，保持跟踪这一页实在内存还是硬盘。问题是这个表本身可能很大，比如若干Mbytes，妨碍虚拟内存到物理内存的快速转换。为了克服这个问题，一张更小的表Translation Look-aside Buffer (TLB)，用于存储最近用到的表信息。当一个虚拟地址能在TLB里找到时，转换速度是很快的。但没有找到时，称为TLB miss，需要重新访问page table。将信息从page table里拷贝到TLB里。TLB可以看做是page table的cache。最近更有些架构中出现类似L2 cache的L2 TLB。 TLB的存在意味着我们需要满足额外的假设

Assumptions (d)：为了保证计算$C_j:=AB_j+C_j$时不会出现TLB miss，$m_c, k_c$必须足够小使得，block矩阵$A$，panel矩阵$B, C$按$n_r$行或$n_r$列拆分成$B_j, C_j$矩阵可以同时被TLB访问
Assumptions (e)：在直到计算完成之前，block矩阵$A$必须一直能被TLB访问。

4.2.3 Packing

通常矩阵$A$是一个大矩阵分解之后的小矩阵，因此矩阵$A$的数据在内存中不是连续的，不连续意味着可能的TLB miss。解决方法是将矩阵$A$ pack成连续数组$\tilde{A}$。适当选择参数$m_c, k_c$使得$\tilde{A}, B_j, C_j$可以容纳在L2 cache里，并且可以同时被TLB访问到。

Case 1: The TLB is the limiting factor

假设系统有$T$个TLB entries，$\tilde{A}, B_j, C_j$对应的TLB entries数目是$T_{\tilde{A}}, T_{B_j}, T_{C_j}$，那么有 $T_{\tilde{A}}+2(T_{B_j}+T_{C_j}) \leq T$

$ T_{B_j}, T_{C_j}$前面有系数2是因为当计算$C_j:=\tilde{A}B_j+C_j$时，TLB需要同时准备好$B_{j+1}, C_{j+1}$ 相比于将$A$加载到L2 cache的开销，将$A$ pack成$\tilde{A}$的操作的开销，不会太大。理由是，packing可以被安排，使得$\tilde{A}$加载到L2 cache和能被TLB访问后，立即能为随后计算使用。前提是，$A$的访问开销不会明显大于将$A$加载到L2 cache，而这一点即使不做$A$没有做pack也是必然的。 GEPP或者GEPM会被分解成GEBP，在之前的case里，block矩阵$B$会在多个GEBP里重用。这就意味着将$B$拷贝成连续数组$\tilde{B}$是有价值的，$B_j$对应的TLB entries数目是$T_{B_j}$也会对应下降到$T_{\tilde{B}_j}$。

Case 2: The size of the L2 cache is the limiting factor.

可以得到case 1类似的结论。

4.2.4 Accessing data contiguously.

为了寄存器更高效的搬移数据，pre-fetch？连续CPU指令需要读取的数据在内存中必须连续。这不仅需要pack，还需要重排。第6章详细介绍。

4.2.5 Implementation of GEPB and GEDOT

类似GEBP

5. PRACTICAL ALGORITHMS

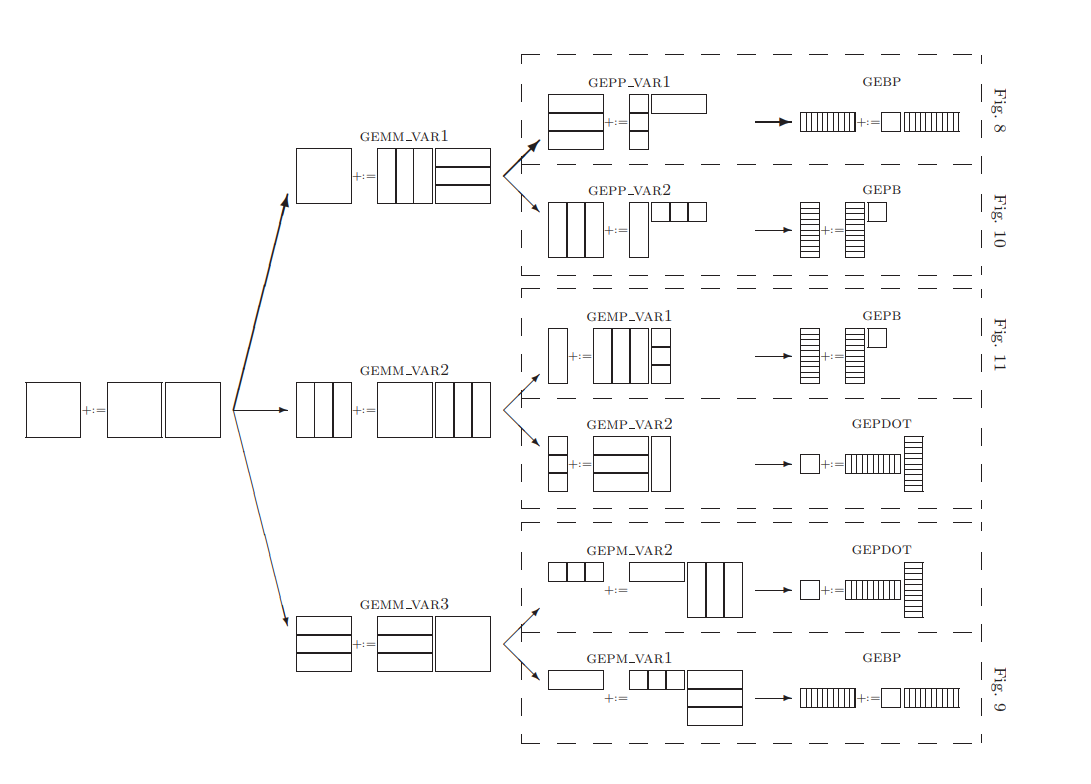
介绍Fig. 4中的6种实现

5.1 Implementing gepp with gebp

Fig8

在gebp_opt1方法中，我们希望$A$一直保留在L2 cache里，$B, C$反复更新在L1 cache，因此需要确定$A$的尺寸最大可以多大，$A$的尺寸上限决定于可用TLB entry数目$\tilde{A}$

将$B$ packing成$\tilde{B}$，$B_j$和$B_{j+1}$各需要一个TLB entry
用$C_{aux}$尺寸是表示着对于这个buffer只需要用到一个TLB entry，$C_j$尺寸是$m_c\times n_r$，如果$m_c$很大的话，每个TLB entry包含一个$m_c$，最多需要$n_r$个TLB entry
那么剩余留给$\tilde{A}$的TLB数目是$T_{\tilde{A}}=T-(n_r+3)$

$C_j$是否连续不是太大的问题，因为这部分数据在GEPP计算时没有重用，只会访问一次。一旦$B$和$A$变成连续的$\tilde{B}$和$\tilde{A}$后，gebp_opt1内的循环计算可以达到浮点运算速度峰值。

packing $B$到$\tilde{B}$的拷贝，是内存到内存的拷贝，开销和$k_c\times n$成正比，分摊到$2m\times k_c\times n$的计算量里，每次拷贝需要$2m$次计算，这种packing操作打乱了之前的TLB上下文。
packing $A$到$\tilde{A}$的拷贝，如果合理编排的话，可以是内存到L2 cache的拷贝，开销和$k_c\times m_c$成正比，分摊到$2m\times k_c\times n$的计算量里，每次拷贝需要$2n$次计算。实际中，这种拷贝不是很耗时。

这种方法适合，$m,n$很大而$k$不大的GEMM类型，如GEPP的定义。

5.2 Implementing gepm with gebp

Fig9

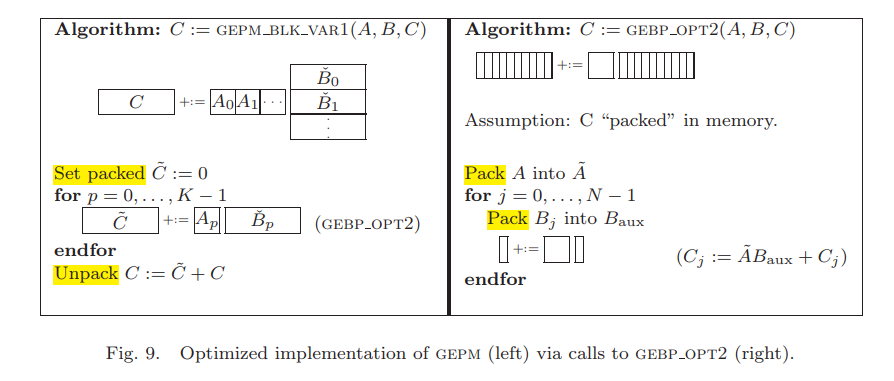
和GEBP不同的是，GEBP中的$C$只需访问一次，而GEPM里的$C$需要反复更新，因此值得将结果加到$C$之前先累加$\tilde{C}=AB$，而不是没计算一次$\tilde{C}=AB$就加到$C$上。$\check{B}p$没有被重用，因此没有pack。此时$B_j$最多需要$n_r$个TLB entry，$B{temp}, C_j, C_{j+1}$各需要一个，那么剩余留给$\tilde{A}$的TLB数目还是$T_{\tilde{A}}=T-(n_r+3)$

5.3 Implementing gepp with gepb

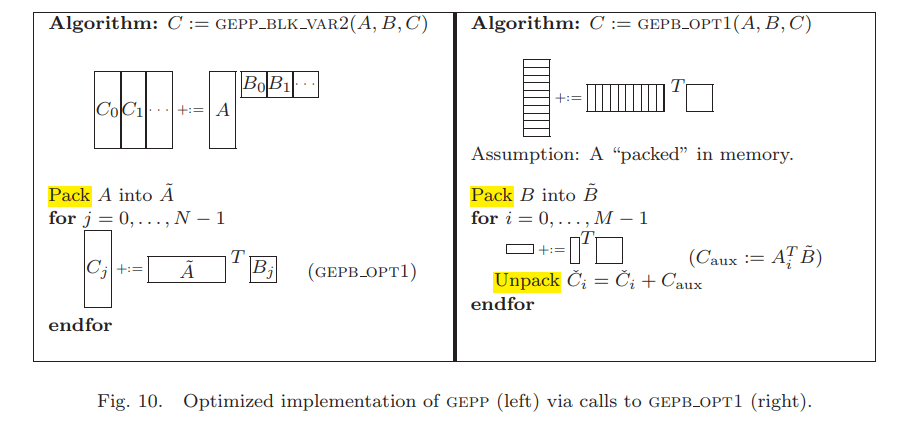
Fig10

$A$做了pack和转置来保证连续访问，在GEPB里$B$做pack而且保存在L2 cache，因此这里我们需要最大化$T_{\tilde{B}}$，同理$T_{\tilde{A}}$的上限是$T-(n_r+3)$

5.4 Implementing gemp with gepb

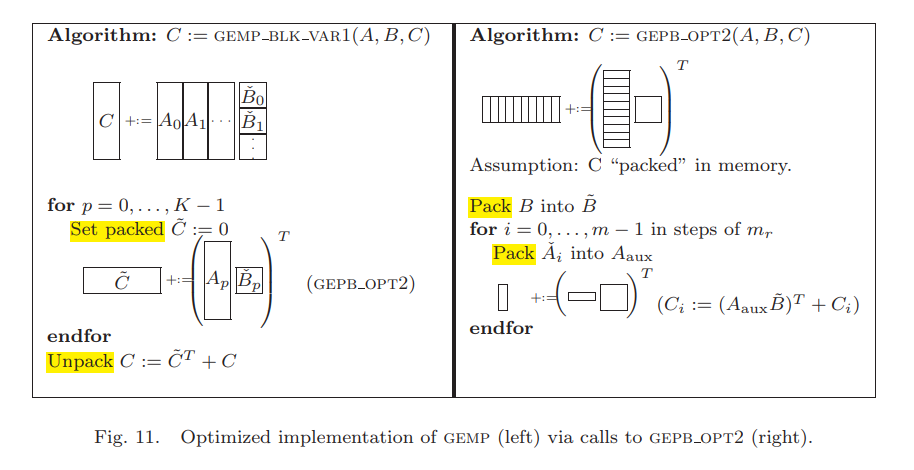
Fig11

用一个临时的$\tilde{C}$来累加$\tilde{C}=(AB)^T$，$\tilde{B}$保留在L2 cache里。同样因此这里我们需要最大化$T_{\tilde{B}}$，$T_{\tilde{A}}$的上限是$T-(n_r+3)$

5.5 Implementing gepm and gemp with gepdot

$C$保留在L2 cache里，每次乘完$A$的一些列和$B$的一些行后累加到$C$上。下面会介绍这种方法不优。

5.6 Discussion

这里我们比较各种实现方法的优劣，结论是gebp实现gepp在列主序情况下最优。首先排除gepdot实现。考量L2 cache带宽，gepdot实现中将$C$保留在L2 cache里，然后从内存里加载$A$和$B$，L2 cache和寄存器时间的带宽是gebp实现的两倍，因此gepdot实现是最差的一种实现。这个结论前提假设是，$A$和$B$的分片$A_j$和$B_j$都太大了，无法保留在L2 cache里。 比较gebp实现gepp Fig.8和gebp实现gepp Fig.9，主要区别在于前者pack $B$而从内存加载$C$，后者从内存加载$B$，将计算之后的临时$\tilde{C}$放在buffer，再unpack $\tilde{C}$并加到$C$里。

gebp实现gepp方法，隐藏从内存读写$C$的开销，而暴露了pack $B$的开销
gebp实现gepp方法，隐藏从内存读$B$的开销，而暴露unpack $C$的开销

预期unpack $C$是比pack $B$更复杂的操作，因此gebp实现gepp比gebp实现gepp更优。同理gepb实现gepp也比gepb实现gemp更优。

最后比较gebp实现gepp和gepb实现gepp，如果矩阵是按照列主序排列的，那么更合适按列分解矩阵，基于此那么gebp实现gepp优于gepb实现gepp。

6. MORE DETAILS YET

我们只关注最优的gebp实现gepp方法。 $C_{m_c,n}+=A_{m_c,k_c}B_{k_c,n}$，其中

$A$是block，$A\in \Bbb{R}^{m_c\times k_c}$
$B$是panel，$B\in \Bbb{R}^{k_c\times n}$
$C$也是panel，$C\in \Bbb{R}^{m_c\times n}$

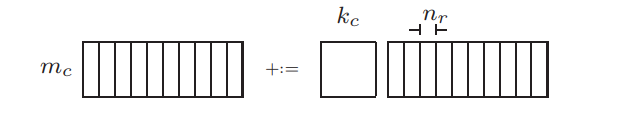
6.1 Register blocking

考虑Fig. 8中的$C_{aux}:=\tilde{A}B$，其中$\tilde{A}$和$B$分别在L2和L1 cache。如下图所示，$C_{aux}$分解成$m_r\times n_r$的子矩阵加载到寄存器里计算。

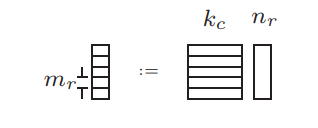
这意味着，计算$C_{j}$的时候不需要子矩阵在L1甚至L2 cache，基于$m_rn_r$ memops 内存操作执行$2m_rn_rk_c$ flops计算量，这里$k_c$选的相对较大。更详细地描述如何将$A$ pack成$\tilde{A}$，在我们的实现里，$A$的尺寸是$m_c\times k_c$，进一步分解成内存连续的$m_r\times k_c$子矩阵，每个子矩阵自身是列主序排列的，那么$C_{aux}:=\tilde{A}B$计算的时候，访问$\tilde{A}$时就是内存连续的了。还有一种实现是将$A$的转置保存成$\tilde{A}$，这种做法复杂度稍微高一些。

6.2 Choosing $m_r\times n_r$

选择 $m_r\times n_r$时有如下考量

一般可用寄存器的一半用于存储$C$分解成的$m_r\times n_r$子矩阵，留剩余寄存器来prefetching $\tilde{A}$和$\tilde{B}$
$m_r\approx n_r$时，加载的开销平摊到计算量上时，即计算密度最优。
如4.2.1章节提到，从L2 cache prefetching $\tilde{A}$到寄存器的开销，不应该比之前的计算开销更长，最理想的是$n_r \geq \frac{R_{comp}}{2R_{load}}$。$R_{comp}=/frac{flops}{cycle}$是CPU浮点运算操作速度，$R_{load}$是L2 cache加载到寄存器的速度

寄存器数目不够会限制gebp_opt1的性能。

6.3 Choosing $k_c$

每加载一个$m_r\times n_r$的$C$子矩阵，都需要和$m_r\times k_c$的$A$子矩阵相乘，为了最大化平摊掉加载开销，$k_c$必须尽量大。但同时$k_c$受以下因素制约

$B_j$会重用很多次，因此最好保留在L1 cache里。同时set associativity and cache replacement policy限制了$B_j$能够占用多少L1 cache。一般，$k_cn_r$个浮点数应该占用少于一般的L1 cache，才能在加载$\tilde{A}$和$C_{aux}$时将$B_j$逐出cache
$\tilde{A}$的尺寸是$m_c\times k_c$应该占据一定比例的L2 cache

经验做法，$k_c$个双精度浮点数占据半页，这样得到的值在各种平台都满足。

6.4 Choosing $m_c$

前面已经讨论了尺寸是$m_c\times k_c$的$\tilde{A}$应该

能被索引TLB
小于L2 cache

事实上还有来自于set associativity and cache replacement policy的限制。 经验做法，$m_c$选择前面限制条件的一半

References

software and the ATLAS project. Parallel Computing 27, 1–2, 3–35. [^4]: Goto, K. and van de Geijn, R. A. 2002. On reducing TLB misses in matrix multiplication. Tech. Rep. CS-TR-02-55, Department of Computer Sciences, The University of Texas at Austin. [^5]: Gunnels, J. A., Gustavson, F. G., Henry, G. M., and van de Geijn, R. A. 2005. A novel model produces matrix multiplication algorithms that predict current practice. In Proceedings of PARA’04. Elsevier.

Gunnels, J. A., Gustavson, F. G., Henry, G. M., and van de Geijn, R. A. 2001. FLAME: Formal linear algebra methods environment. ACM Transactions on Mathematical Software 27, 4 (December), 422–455. ↩ ↩² ↩³
Agarwal, R., Gustavson, F., and Zubair, M. 1994. Exploiting functional parallelism of POWER2 to design high-performance numerical algorithms. IBM Journal of Research and Development 38, 5 (Sept.). ↩
Whaley, R. C., Petitet, A., and Dongarra, J. J. 2001. Automated empirical optimization of ↩