1 语音唤醒技术简介

语音唤醒，或者说关键词检测，是语音识别任务的一个分支，需要从一串语音流里检测出有限个预先定义的激活词或者关键词，而不需要对所有的语音进行识别。这类技术是使能嵌入式设备语音交互能力的基础，可以被应用到各种领域，比如手机，智能音箱，机器人，智能家居，车载设备，可穿戴设备等等。唤醒词预先设定，大部分中文唤醒词是四字，音节覆盖越多，音节差异越大，相对唤醒和误唤醒性能越好，也有些技术领先的算法公司可以做到三字或者二字唤醒词。当设备处于休眠状态时，持续拾音持续检测唤醒词，一旦检测到唤醒词，设备从休眠状态切换到工作状态等待后续交互。作为一种基础应用，语音唤醒任务主要从两个维度考量

唤醒性能唤醒性能主要包括召回率 TPR和虚警率 FPR。召回率是指正确识别的正例数据在实际正例数据中的百分比，也就是正确被唤醒次数占总的应该被唤醒次数的百分比。虚警率是指错误识别的负例数据在实际负例数据中的百分比，也就是不该被唤醒却被唤醒的概率。这两者通常是此消彼长的关系，一个指标提升带来另一指标的下降。根据使用场景的不同，这两者的侧重点也会有所不同。
复杂度复杂度主要体现在计算和内存开销上，因为设备处于持续拾音和持续检测的状态，需要较低的响应时延来保证用户体验，同时由于多数嵌入式设备依赖电池，较低的功耗才能保证合理的待机时间，要求更少的计算和内存开销。

目前常用的系统框架主要有基于HMM隐马尔科夫模型和基于神经网络两种。

基于HMM隐马尔科夫模型¹ 这种方法与传统LVCSR（大规模词表语音识别）方法类似，区别在于解码网络的大小。因为不需要识别所有语音，因此解码网络不需要包含字典所有词汇，只需要包含激活词，这样的网络会比语音识别的网络小很多，有针对性地对关键词进行解码，可选的路径就少了很多，解码的速度也会得到大幅度的提升。对于解码出来的候选再作一个判断。
基于神经网络随着机器学习在图像领域的日益流行，神经网络也逐渐应用到语音领域，相比于前一种方法，这里不再需要解码步骤，实现了端到端的输出，也就是输入语音，输出关键词。

图12-1 基于神经网络的语言唤醒流程

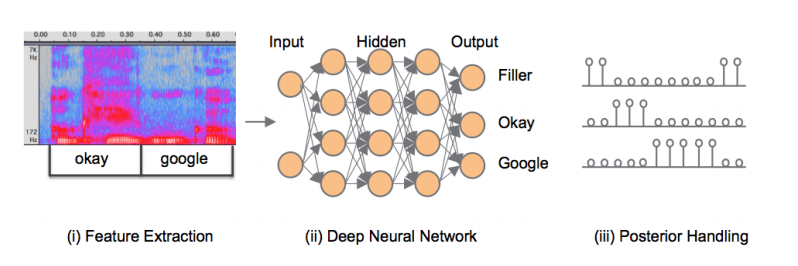
图1所示是目前主流的方法，具体流程是

从语音信号里提取特征
经过一个神经网络，输入语音特征，输出激活词后验概率
对于后延概率做一个平滑，判决是否激活

将在下一章中重点讨论特征提取和神经网络结构。

2 特征提取

与其他机器学习的任务类似，特征提取对于模型训练来说至关重要，目前最常用的语音特征提取方式是滤波器组Fbank和MFCC。

2.1 Fbank

Fbank包含如下步骤

预加重滤波器

预加重处理其实是一个高通滤波器，目的是提升高频部分，使信号的频谱变得平坦，保持在低频到高频的整个频带中，能用同样的信噪比求频谱。同时，也是为了消除发生过程中声带和嘴唇的效应，来补偿语音信号受到发音系统所抑制的高频部分，也为了突出高频的共振峰。

\[y(t)=x(t)-\mu x(t-1) \tag{12-1}\]

其中$\mu$值介于$0.9 - 1$之间

语音分帧

语音信号的频率是时变的，如果在整段语音信号上做傅里叶变换的话，会失去这个时变的包络信息。但是在很短的时间片段内，可认为语音信号频率是稳定的，因此基于一个短时片段做傅里叶变换，可以近似得到信号的频域包络。将一个包含$N$个采样点的短时片段称为帧，帧长通常为10~30ms左右。为了避免相邻两帧的变化过大，会让两相邻帧之间有一段重叠区域，此重叠区域包含了$M$个取样点，通常$M$的值约为$N$的$\frac{1}{4}$至$\frac{1}{3}$。通常语音识别所采用语音信号的采样频率为8kHz或16kHz，以16kHz来说，若帧长度为256个采样点，则对应的时间长度是$256/16000×1000=16ms$。值得注意的是，窗长的选择是频率分辨率和时间分辨率的折中，窗长越大，带宽越小，频率分辨率越明显，但时间分辨率越模糊。窗长越小则结论相反。

加窗

上一步分帧的操作相当于在连续的语音流上加了矩形窗截取出有限长片段，应用矩形窗相当于时域相乘，频域卷积，导致在频域除了应有主瓣外，还产生了不该有的旁瓣，称之为频谱泄漏。为了减小频谱泄漏，会用到一些旁瓣衰减更大的窗函数，比如汉明窗和高斯窗。如下图所示，矩形窗的旁瓣非常严重，而高斯窗和汉明窗对旁瓣有一定压制作用，减弱频谱泄漏带来的影响。

图12-2 矩形窗

图12-3 高斯窗

图12-4 汉明窗

短时傅里叶变换STFT

基于每一帧做$N$点的FFT，称之为短时傅里叶变换Short-Time Fourier-Transform (STFT)，$N$的典型值是256或者512。基于如下公式计算功率谱密度，其中$x_{i}$是原始语音$x$的第$i$帧：

\[P=\frac{|FFT(x_{i})|^{2}}{N} \tag{12-2}\]

梅尔频域滤波器组

在语音唤醒任务里，通常采用一组滤波器提取特征，在一定程度上逼近人耳拾音特点，从而提高唤醒识别的准确性。主要涉及两个人耳特性来帮助设计滤波器组：

频域感知非线性，指导滤波器组的中心频率
掩蔽效应和临界带宽，指导滤波器组的带宽

人耳对不同频率的声音敏感度不同，就像一个滤波器组一样，它只关注某些特定的频率分量，也就说，它只让某些频段信号通过，而无视它不想感知频段信号。高频和低频的敏感度比较低，如下图所示，30Hz和15kHz的声音需要60dB才能被人耳听到，而1kHZ的声音在0db处就可以听到。

图12-5 人耳频率敏感度

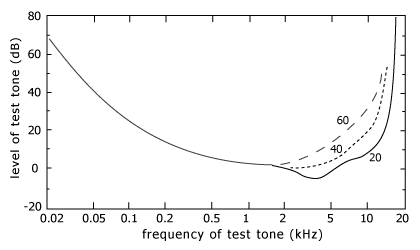
同时在感知频率区域内，敏感度也不是均匀分布的，比如在$(100Hz\sim 4kHz)$区域内曲线比较平缓，而5kHz以上曲线就变得陡峭。针对人耳敏感度在频域的这种非线性，将语音转换到梅尔Mel刻度，梅尔刻度是一种基于人耳对等距的音高变化的感官判断而定的非线性频率刻度，梅尔刻度和赫兹的转换关系是

\[m=2595\; log_{10}(1+\frac{f}{700}) \\ f=700\; (10^{\frac{m}{2595}}-1) \tag{12-3}\]

在梅尔频域内均匀分布滤波器组，正好线性反映了人耳对音调的感知能力。人耳在安静的环境中分辨出轻微的声音，但是在嘈杂的环境里，这些轻微的声音就会被杂音所淹没，这个重要特性称为掩蔽效应，举例来说，假设安静环境下听清某声音A的最小分贝是35db，如果此时同时存在另一声音B，由于声音B的存在，听清声音A的最小分贝是40db，比安静环境下提高了5db。此时称声音B为掩蔽声，声音A为被掩蔽声，40db称为掩蔽阈。当两个频率相近的声音同时存在时，两者可能发生掩蔽效应，人耳会把两个声音听成一个。临界带宽指的就是这样一种令人的主观感觉发生突变的带宽边界，当两个声音的频域距离小于临界带宽时，就会产生屏蔽效应。将滤波器组带宽设置为临界带宽，就能模拟人耳的这一特性。基于以上信息，可以设计一组基于梅尔频域的三角滤波器，滤波器个数接近临界带宽个数，中心频点在梅尔频域均匀分布，来模拟人耳特性。

图12-6 基于梅尔频域的三角滤波器

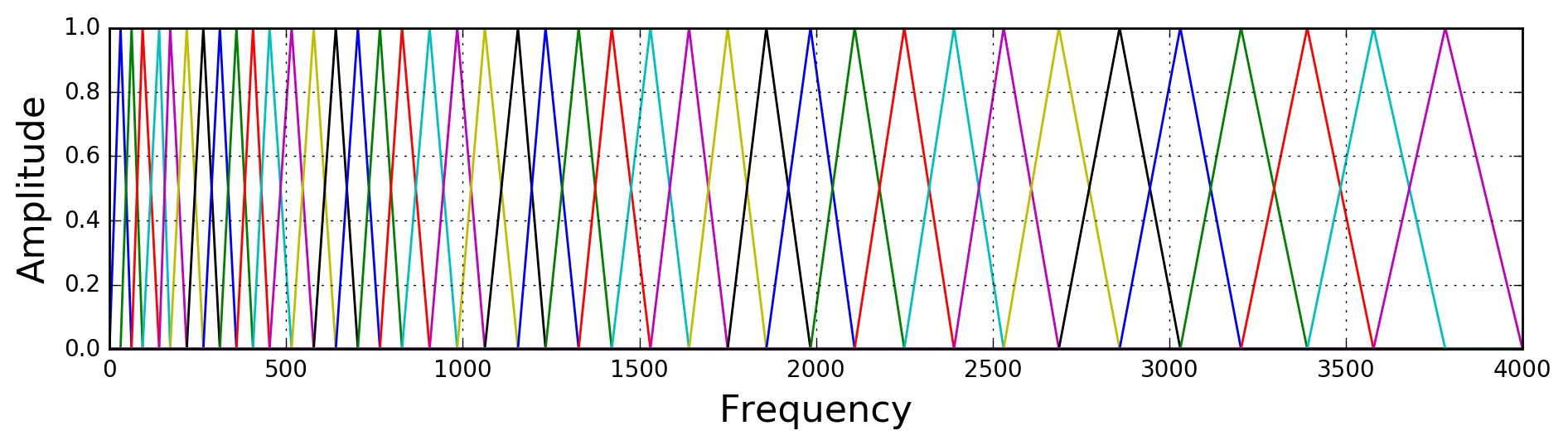
经过梅尔频域滤波器组之后，可以得到如下语谱图，用二维图像信息表达三维语音信息。语谱图的横坐标是时间，纵坐标是频率，坐标点值为语音数据能量，颜色越深，则该点语音能量越强。

图12-7 语谱图

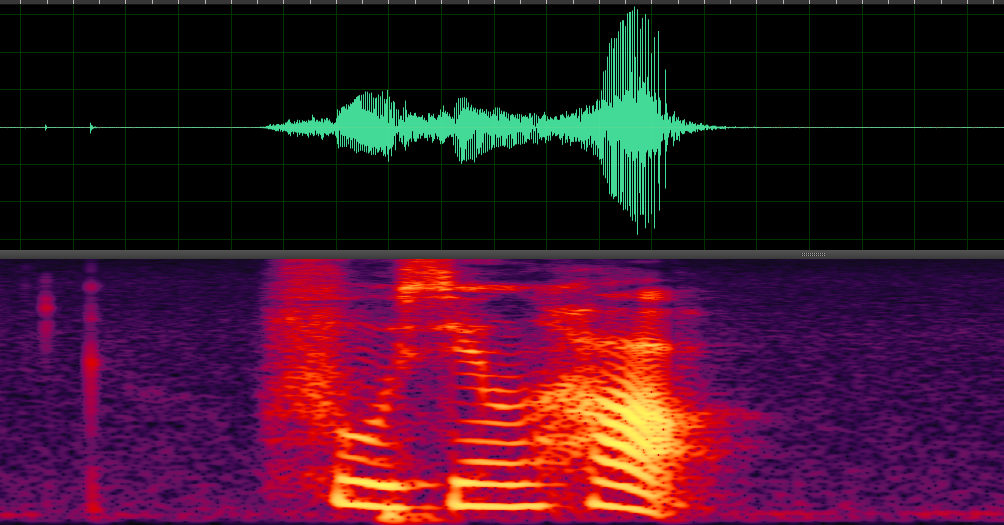
2.2 MFCC

MFCC包含完整的FBank操作，在此基础上额外增加了离散余弦变换DCT。基于上一步FBank得到的频谱对数坐标域上做DCT，相当于做逆FFT转换回时域，因此称为倒谱Cepstrum。从频域转换到倒谱域主要出于两点考虑

去相关性 FBank特征之间是高度相关的，DCT用于去除各维特征之间的相关性。
数据压缩 DCT的输出维度和输入维度相同，倒谱低频信息体现了包络，这对语音唤醒任务比高频信息更重要，因此输出维度实际可以不用全部保留，比较典型的是保留2到13维，一定程度上实现了数据量的压缩。

MFCC只能反映语音的静态特征，而动态特征可以用这些静态特征的一阶差分或者二阶差分来描述。此外除了倒谱信息，还可以加入其它语音特征，比如音高和过零率。

基本上整个FBank/MFCC的处理流程都在尽量模拟人耳的特性，相当于有一个丰富先验知识的专家网络用来提取特征。目前已经有一些论文讨论，类似图像任务一样，让神经网络自主的从时域信号里提取特征，而不是靠专家知识。

2.3 PCEN

FBank或者MFCC一般会在最后一步取对数来压缩动态范围，但是取对数之后，放大了小幅值的动态范围，而压缩了大幅值的动态范围，比如安静语音幅值会占据大部分动态范围。其次FBank/MFCC值和语音响度强相关，比如同样一段语音，音量放大或者缩小，会得到完全不同的FBank/MFCC值，而预期音量不应该对唤醒结果造成影响。基于此，google在2016年提出信道能量归一化的特征PCEN (per-channel energy normalization) ² 。 PCEN计算公式如下 $PCEN(t,f)=(\frac{E(t,f)}{(\epsilon +M(t,f))^\alpha}+\delta)^r-\delta^r \\ M(t,f)=(1-s)M(t-1,f)+sE(t,f) \tag{12-4}$

这里$E(t,f)$是原始FBank特征，$M(t,f)$是采用一阶无限滤波器平滑之后的FBank特征，其中$s$是平滑系数，$\epsilon$是一个防止除数为0的极小值，一般$\epsilon=10^{-6}$。 $E(t,f)/(\epsilon +M(t,f))^\alpha$部分实现了一个前馈AGC，归一化强度由$\alpha$控制，$\alpha \in[0,1]$，值越大归一化程度越大。通过归一化消除了响度影响。这里的归一化操作是基于通道的。AGC之后用开方来压缩动态范围。 PCEN的另一个重要优点是可微分的，那就意味着公式里的超参数是可训练的，可以作为模型结构中的一层加入训练。试验证明训练得到的PCEN参数比固定PCEN参数性能更优，同时也超过FBank模型性能。

3 模型结构

传统的语音唤醒是基于HMM加序列搜索方法，近年来基于神经网络的方法大量应用于语音识别任务，唤醒任务作为语音识别任务的一个分支，借鉴了很多模型结构，同时基于本身资源开销小，任务相对简单，基于远场语音等特点，相应做了优化改进。

3.1 DNN

google比较早地在2014年提出用深度神经网络deep neural networks的方法来实现语音唤醒，称之为Deep KWS ³。如下图所示，唤醒分为三个步骤，

图12-8 google kws识别方法

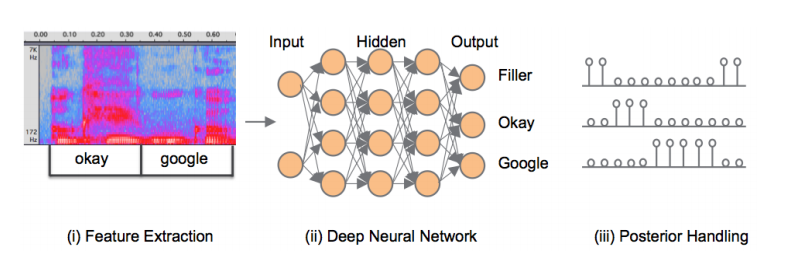
首先对输入语音做特征提取，然后经过DNN网络得到一个三分类的后验概率，三分类分别对应关键字Okey，Google和其他，最后经过后处理得到置信度得分用于唤醒判决。

特征提取

出于减少计算量的考量，这里包含了一个VAD检测机制，用一个13维的PLP特征和他们的一阶差分二阶差分通过一个高斯混合模型 GMM得到每帧人声和非人声的后验概率，再通过平滑和阈值判断决定出人声范围。在人声范围内，基于25ms窗长和10ms窗移得到40维FBank特征。每次输入给模型的特征都在当前帧基础上前后拼接了一部分状态，权衡计算量，时延和精度，Deep KWS在实现中向前拼接了10帧，向后拼接了30帧。

神经网络

网络结构部分用的是标准的全连接网络，包含$k$层隐层，每层隐层包含$n$个节点和RELU作为激活函数，最后一层通过softmax得到每个标签的后验概率。Deep KWS的标签只用来表示完整词，即完整包含整个激活词作为一个标签，这些标签来自于一个50M LVCSR大模型的强制对齐。相比于非完整词sub-word标签，完整词标签的好处是， - 减少最后一层的网络参数 - 使得后处理更简单 - 更好性能训练中采用交叉熵作为损失函数，同时提到，可以复用其他语音识别网络结构来初始化隐层，实现迁移学习，避免训练陷入局部最小值从而提高模型性能。

后处理判决

得到基于帧的标签后验概率之后，后处理部分将后验概率经过平滑处理，得到唤醒置信度得分。平滑过程是为了消除原始后验概率噪声，假设$p'_{ij}$是原始后验概率$p'_{ij}$平滑之后的结果，平滑窗口为$w_{smooth}$，平滑公式如下

\[p'_{ij}=\frac{1}{j-h_{smooth}+1}\sum_{k=h_{smooth}}^j p_{ik} \tag{12-5}\]

其中$h_{smooth}=max\{1,j-w_{smooth}+1\}$，是平滑窗$w_{smooth}$内的最早帧号索引。然后基于平滑之后的后验概率$p'_{ij}$计算得到置信度，在一个滑动窗$w_{max}$第$j$帧的置信度

\[confidence=\sqrt[n-1]{\prod_{i=1}^{n-1}\max \limits_{h_{max}<k<j}p'_{ik}} \tag{12-6}\]

其中$h_{max}=max\{1,j-w_{max}+1\}$，是平滑窗$w_{max}$内的最早帧号索引。计算得到的置信度和预定义的阈值比较，做出唤醒判决。Deep KWS中使用的$w_{smooth}=30$和$w_{max}=100$，能得到相对较好的性能。

3.2 CNN

在过去几年里，卷积神经网络 CNN越来越多的应用在声学模型上，CNN相比于DNN的优势在于

DNN不关心频谱结构，输入特征做任何拓扑变形也不会影响最终性能，然而频谱在时频域都有高度相关性，CNN在抓取空间信息方面更有优势
CNN通过对不同时频区域内的隐层节点输出取平均的方式，比DNN用更少的参数量，克服不同的说话风格带来的共振峰偏移问题

google在2015年提出基于CNN的KWS模型⁴，典型的卷积网络结构包含一层卷积层加一层max池化pooling层。

图12-9 CNN模型结构

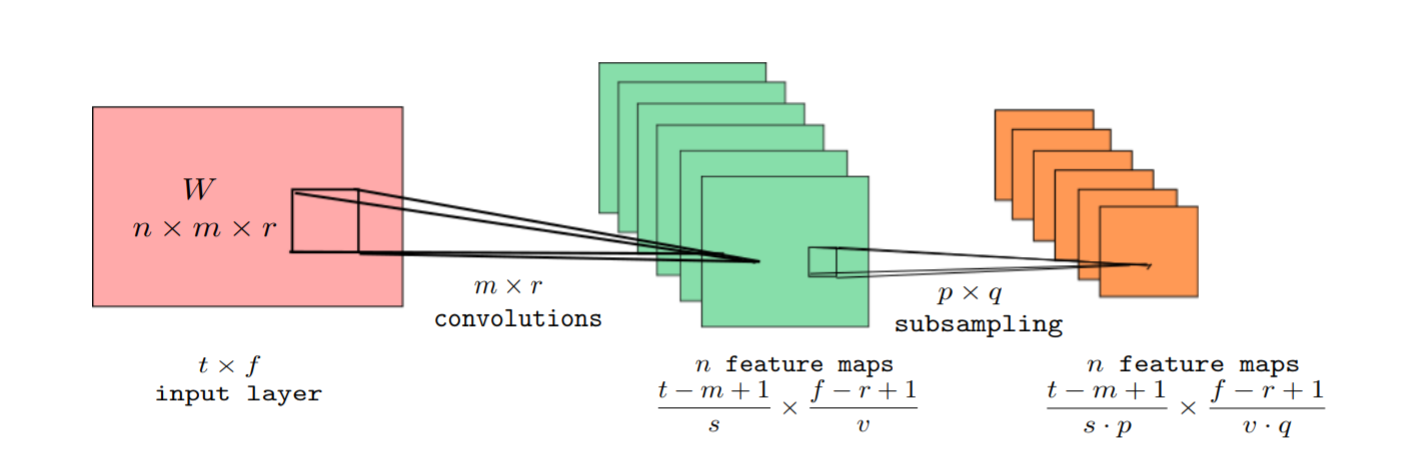
这里输入特征$V$的时域维度是$t$，频域维度是$f$，经过一个$n$个$(m\times r)$的卷积核，同时卷积步长是$(s,v)$，输出$n$个$(\frac{(t-m+1)}{s}\times \frac{(f-r+1)}{v})$的feature map。卷积之后接一个max池化层提高稳定性，这里pooling降采样系数是$(p\times q)$，那么最终输出feature map是$(\frac{(t-m+1)}{s\dot p}\times \frac{(f-r+1)}{v\dot q})$。这里给出一个250K参数量的模型，包含2层卷积结构，一层线性低阶，一层全连接层，具体参数如下

type	m	r	n	p	q	Par.	Mul.
conv	20	8	64	1	3	10.2K	4.4M
conv	10	4	64	1	1	164.8K	5.2M
lin			32			65.5K	65,5K
dnn			128			4.1K	4.1K
softmax			4			0.5K	0.5K
Total						244.2K	9.7M

在此基础上一系列的参数实验得出一些经验

保证同等误激活和参数量前提下，CNN模型比DNN模型性能提高40%以上。
随着pooling长度$p=1$到$p=2$，安静和噪音下唤醒性得到提升，但是$p=3$之后没有明显改善。
同等计算量条件下，卷积核滑动尽量重叠。比如对比卷积核$(32\times 8\times 186)$，步长$(1,4)$，和卷积核$(32\times 8\times 336)$，步长$(1,8)$，两者计算量近似，但前者性能远超后者。
在必须减少模型计算量情况下，增大卷积核滑动步长优于增加pooling。
在时域滑动$s>1$都会影响性能，而卷积核步长$s=1$后面接pooling，可以在降采样之前针对相邻帧关系更好的建模，比直接卷积核步长$s>1$更有效。

3.3 CRNN

CNN建模的一个缺陷是，一般尺寸的卷积核不足以表达整个唤醒词上下文，而RNN正好擅长基于上下文建模。RNN的缺点在于学不到连续频谱的空间关系，而CNN正好擅长基于空间关系建模。因此语音任务中出现将CNN和RNN结合的CRNN模型结构，并以CTC作为loss函数，baidu将这个模型结构应用在唤醒任务上，并大幅缩减了模型参数量。CRNN的网络结构如下图所示

图12-10 CRNN模型结构

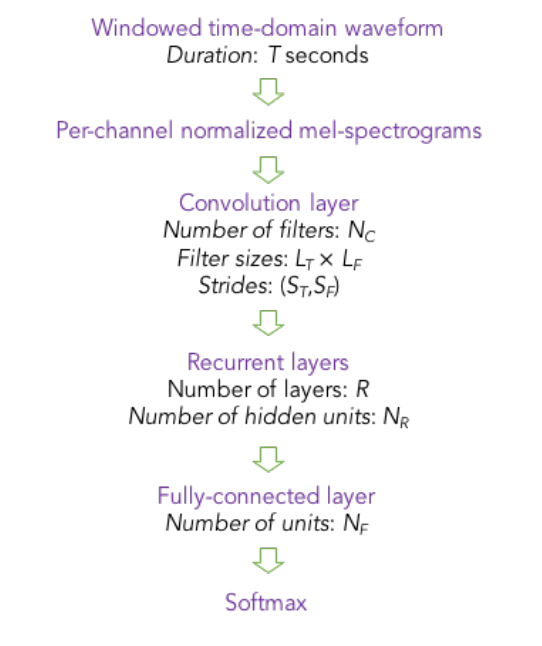
出于减少复杂度的考量，训练中的标签指示当前帧是否包含唤醒词，语音识别任务中的CTC损失函数被替换成开销更小的CE损失函数⁵。从CTC损失函数到CE损失函数，给训练任务带来的重要变化就是训练样本需要精确严格的对齐，需要由一个更大的识别模型预先得到唤醒词在训练样本中的出现和结束时间点。增大卷积核数目和增大RNN节点数目可以显著提高模型性能，RNN层选择GRU比LSTM计算量更小而且性能更好，但是增加RNN层数对提高性能几乎没有帮助。

3.4 DSCNN

机器视觉任务中，深度可分离卷积结构(depthwise separable convolution DSCNN)在许多领域逐渐替代标准三维卷积。DSCNN相比于普通CNN，能够显著降低参数量和计算量。DSCNN最早在google的Xception⁶和MobileNet⁷中提出，核心思想是将一个完整的卷积运算分解为两步进行，分别为Depthwise Convolution与Pointwise Convolution。

图12-11 DSCNN与普通CNN对比

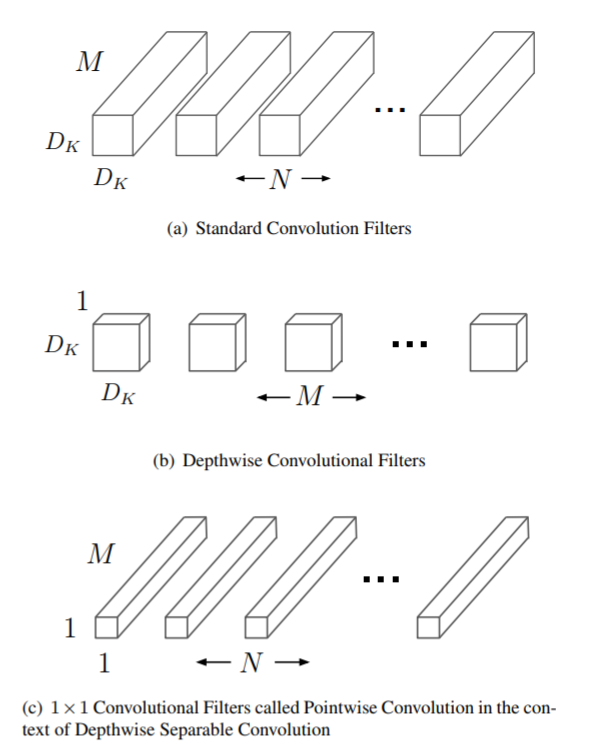
假设一个卷积输入尺寸是$D_F×D_F×M$，输出尺寸是$D_F×D_F×N$，$D_F$ 指特征的长和宽，那么

普通卷积核$D_K×D_K$ 输出一共有$D_F×D_F×N$个点，对于输出的每一个点，都要做$D_K×D_K×M$次乘法，再把个$M$个通道叠加，总计算量是$D_K×D_K×M×D_F×D_F×N$
DSCNN
- Depthwise convolution 针对每个输入通道采用不同的卷积核，就是说一个卷积核对应一个输入通道，卷积核一共有$D_K×D_K×M$，输出一通道的乘法次数是$D_K×D_K×D_F×D_F$，输出$N$通道的计算量是$D_K×D_K×D_F×D_F×M$
- pointwise convolution 普通卷积，只是卷积核的尺寸为$1×1$，卷积核数目是是上一层的输出通道数。所以这里的卷积运算会将上一步的输出在深度方向上进行加权组合，生成新的Feature map。计算量维$M×D_F×D_F×N$

比较DSCNN和标准卷积的计算量 $\frac{(D_K×D_K×M×D_F×D_F+M×D_F×D_F×N)}{(D_K×D_K×M×D_F×D_F×N)}=\frac{1}{N}+\frac{1}{D_K^2} \tag{12-7}$

一般情况下，$N$较大，$\frac{1}{N}$ 可以忽略，那么比如$3×3$的卷积核，DSCNN可以降低9倍计算量。

图12-12 DSCNN模型结构

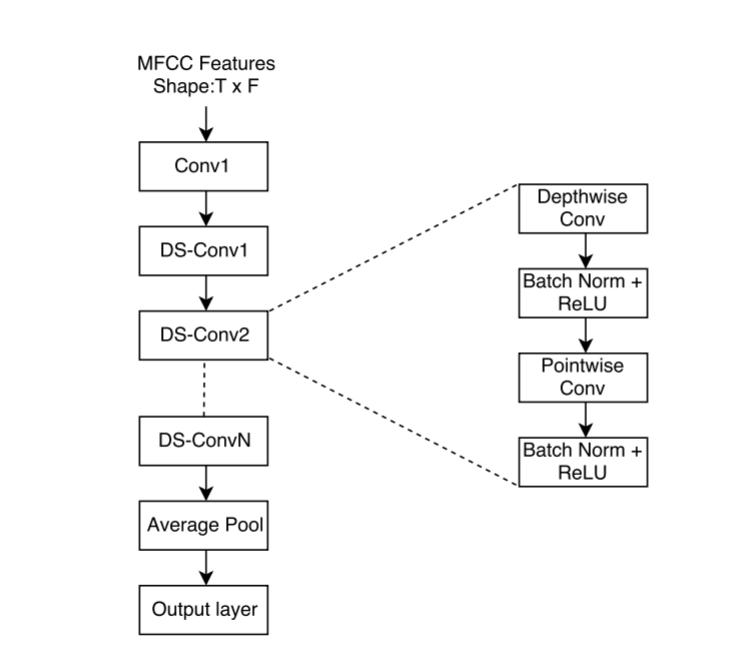
DSCNN应用于唤醒任务的模型结构如上图所示，在DSCNN层之后加一层pooling和全连接层，用于减少参数量并提供全局连接⁸。

3.5 Sub-band CNN

在特征提取章节提到，人耳对不同频带敏感度不一样，于是就有基于不同频谱子带用卷积提取特征的方法⁹。

图12-13 Sub-band CNN模型结构

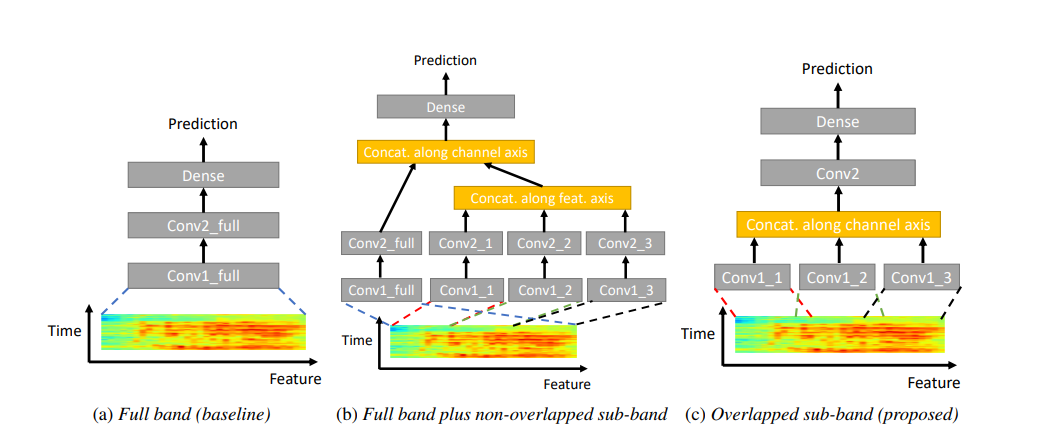
首先输入特征被分成$B$个子带，图中$B=3$，每个子带应用一组卷积核，基于子带提取出的特征合并，作为下一层卷积层的输入，最后经过一层全连接层输出预测概率。频谱子带如何划分和子带提取特征如何再组合是子带CNN的重点

子带划分子带划分有两种选择，子带之间重叠或者不重叠。子带不重叠可能引入边界频点信息丢失，而子带重叠方法又会带来额外的计算量。
子带提取特征再组合特征再组合方式有
- 各子带独立经过卷积层1提取特征，沿着通道维度组合，再经过卷积层2和全连接层
- 各子带独立经过卷积层1和2，合并作为输入经过全连接层，这里作为全连接层的输入，就没有组合方式选择的问题。
- 各子带独立经过卷积层1提取特征，沿着频率维度组合，再经过卷积层2和全连接层

实验结果显示，得益于卷积层2感受野的扩大，第一种沿着通道维度组合性能最优。通常需要堆叠多层卷积来增大感受野，而Sub-band CNN提供一种更低成本的感受野扩大方式，适合唤醒任务低开销的特点。

3.6 Attention

以上介绍的方法虽然可以把模型结构做到很小，但是需要一个预先训练的更大声学模型来完成帧级别的对齐工作。基于attention的模型可以做到完整的端到端训练，也就是不需要预先对齐¹⁰。

图12-14 Attention模型结构

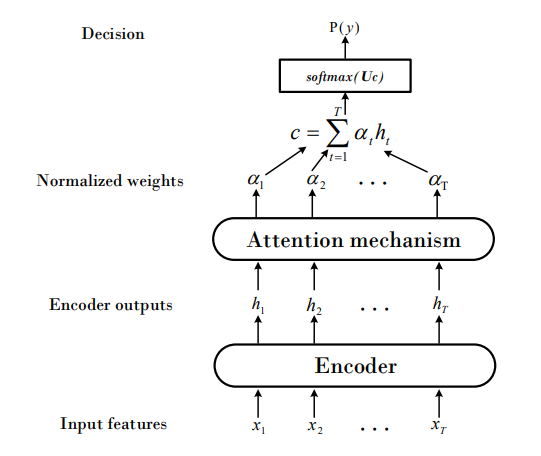
模型结构由两部分组成，Encoder和Attention。Encoder的作用是将声学特征转换到更高维的表达，Encoder的结构可以由不同网络类型组成，比如LSTM，GRU或CRNN。假设输入语音特征是${\bf{x}}=( x_1, ..., x_T)$，经过encoder之后得到高维表达${\bf{h}}=( h_1, ..., h_T)$，

\[{\bf{h}}=Encoder({\bf{x}}) \tag{12-8}\]

Attention基于Encoder生成的高维表达$\bf{h}$，得到一组归一化权重

\[\alpha_t=Attend(h_t) \tag{12-9}\]

将这组权重应用于高维表达${\bf{h}}$，得到一组定长向量${\bf{c}}$

\[{\bf{c}}=\sum_{t=1}^T \alpha_th_t \tag{12-10}\]

最后基于这组定长向量，经过前行变换${\bf{U}}$和softmax得到概率分布

\[p(y)=softmax({\bf{Uc}}) \tag{12-11}\]

这里Attention由两种方式

Average attention 不包含可训练参数，相当于$\bf{h}$向量取均值

\[\alpha_t=\frac{1}{T} \tag{12-12}\]

Soft attention 这里$\alpha_t$不再固定，而是通过训练得到，这种方法相比于取均值方法，在很多其他应用attention的任务中被证明更有效。

\[e_t=v^Ttanh({\bf{W}}h_t+{\bf{b}}) \\ \alpha_t=\frac{exp(e_t)}{\sum_{j=1}^T exp(e_j)} \tag{12-13}\]

4 计算加速

4.1 硬件资源评估

首先需要指标来评估硬件平台性能和模型或者算法开销，当硬件平台性能满足模型或者算法开销时，这个模型在这个平台上是可执行的。评估硬件平台性能或者模型开销一般会用到两个硬件资源指标，算力和带宽

算力，单位是FLOP/S，floating-point operations per second，指示这个硬件平台在理想状况下，每秒钟可以完成的浮点运算数。
带宽，单位是Byte/s，指示这个硬件平台在理想状况下，每秒可以完成的内存读写量。

那CONV2D为例，输入$[N,H,W,C_{in}]$，卷积核$[K_H,K_W,C_{in},C_{out}]$，假设padding方式为same，输出$[N,H,W,C_{out}]$

算力开销为

\[N\cdot H\cdot W\cdot K_H\cdot K_W\cdot C_{in}\cdot C_{out} \quad {\rm {FLOP}} \tag{12-14}\]

卷积计算方式的带宽开销为，读输入+读参数+写输出

\[N\cdot H\cdot W\cdot C_{in} + K_H\cdot K_W\cdot C_{in}\cdot C_{out} + N\cdot H\cdot W\cdot C_{out} \quad {\rm {4 bytes}} \tag{12-15}\]

这里假设硬件缓存足够大，所有数据都可以被cache住，只需要读取一次，不需要重复从内存读取。而事实上在嵌入式设备中，这是不可能做到的。

由算力和带宽进一步衍生出计算密度

计算密度单位是FLOP/byte，加载一个byte可以做多少次运算

下面这个图反应的是，横坐标是计算密度，纵坐标是算力，在一个硬件平台中，一开始算力随着计算密度的增加线性增加，也就是说一开始喂得数据越多，运算处理的越快，但增大到一定程度时，算力就不再增长了。观察到的现象是，一开始随着计算量的增加，运行时间几乎不变，但当算力维持不变时，运行时间就随着计算量的增加线性增加。前半段曲线是带宽受限，这个区间内的目标是提高算力，让模型运行在尽可能接近顶部位置，后半段是算力受限，这个区间内算力已经达到顶点，目标是减低计算量。

图12-15 算力带宽模型

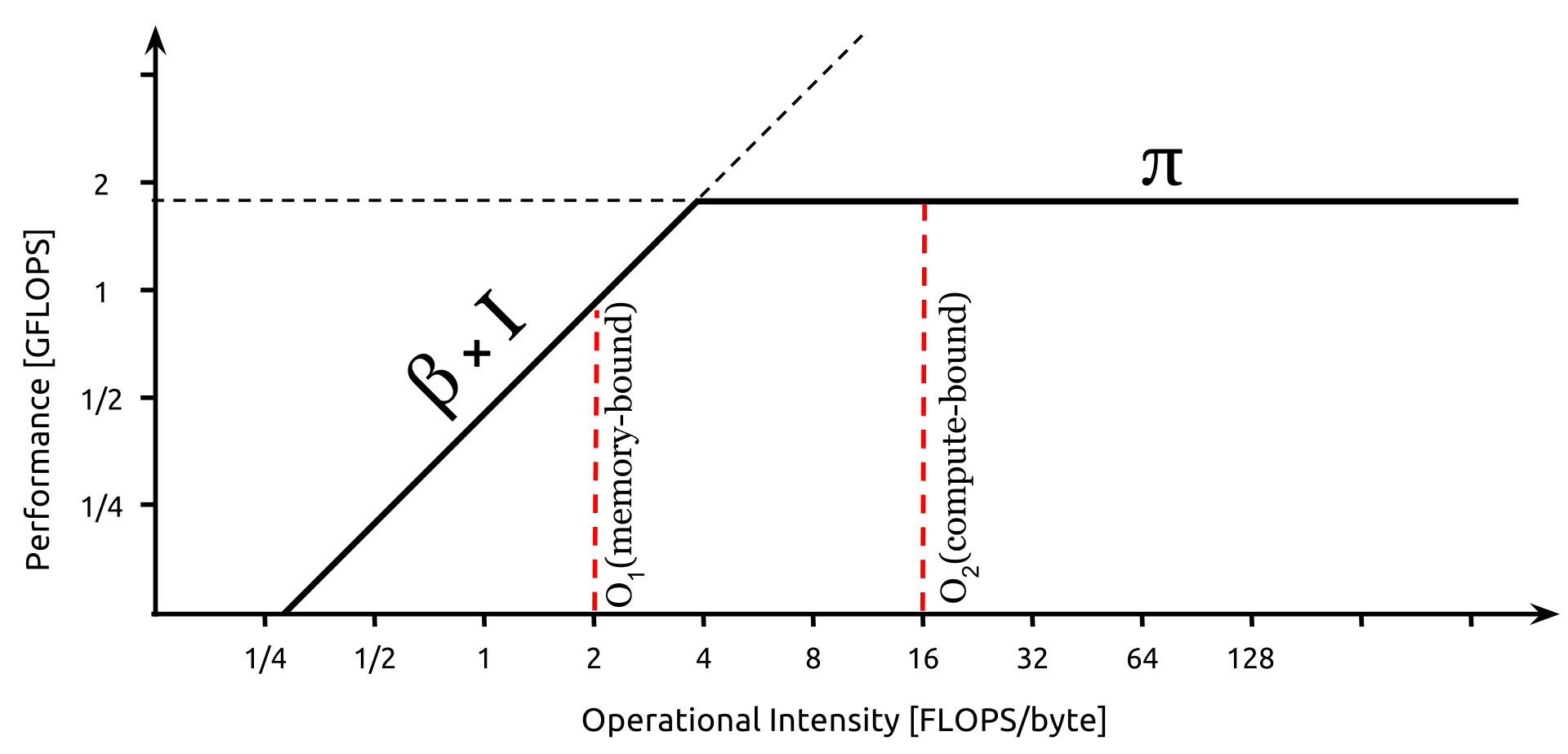
下面比较了两种不同类型运算的计算密度

矩阵乘矩阵， $C_{1000,1000}=A_{1000,1000} \times B_{1000,1000}$
- 算力开销，输出每一个点需要1K次乘加操作，一共需要2G FLOP
- 带宽开销，读两个矩阵，写一个矩阵，每个矩阵4M bytes，至少需要12M bytes
- 计算密度，2G FLOP/12M bytes = 170 FLOP/MBytes
矩阵乘向量，$C_{1000,1}=A_{1000,1000} \times B_{1000,1}$
- 算力开销，输出每一个点需要1K次乘加操作，一共需要2M FLOP
- 带宽开销，读一个矩阵，忽略读写两个向量，每个矩阵4M bytes，至少需要4M bytes
- 计算密度，2M FLOP/4M bytes = 0.5 FLOP/MBytes

那么明显矩阵乘矩阵是受限于算力的，矩阵乘向量是受限于带宽的，两者的优化方向是不同的。

这是一个计算机的存储器层次结构。越接近CPU的存储器越快也越昂贵。最接近CPU的寄存器访问速度最快，可以被算数指令直接访问，次一级的cache访问速度较快，容量比寄存器大一些。通常意义的数据或者模型都是在RAM里，通常速度是跟不上CPU的速度的。

图12-16 计算机存储器层次结构

在带宽受限的场景里，需要合理的运用有限的寄存器和cache资源，使得算力尽可能接近顶点。

举个例子，cache资源在各种计算平台差距很大，NVIDIA tesla V100有36MB片上cache，一般智能音箱嵌入式平台有4KB，MCU平台没有片上cache。因此普遍的嵌入式设备是没法一次性把3个 $C_{1000,1000}$矩阵cache起来，而是需要反复加载同一段内存到cache，用于CPU计算，CPU在很多时候都出于等待状态。因此像矩阵乘矩阵这样的操作，在嵌入式设备上不仅仅受限于算力的，也同样受限于带宽。

4.2 加速方向

由上文提到的硬件资源指标，可以大致归纳出如下加速方向

降低计算量：fft/winograd加速卷积，稀疏化
降低带宽：gemm，im2col加速卷积
同时降低计算量和带宽：低精度运算

需要注意的是，很多方法是内存占用和计算量/带宽之间的平衡，用更多的内存占用来换取更少的计算量或更低的带宽占用，例如fft/winograd方法，会一定程度上展开内存。在很多嵌入式设备上，没有足够内存来实现这些加速方法，这是加速之外的另一个维度的考量。

4.2.1 GEMM

神经网络前向计算中，绝大多数计算量都在于矩阵乘加，比如全连接和RNN操作，完全就是矩阵乘加操作。卷积操作复杂一些，一方面是通过重排，将卷积转换成矩阵乘加，另一方面通过变换，降低计算量。矩阵乘加操作加速是应用最广泛适用的方法，先对矩阵根据尺寸做一个分类

matrix: 两个维度尺寸都很大
panel: 一个维度尺寸很大
block: 两个维度尺寸都很小

\[C_{m,n} += A_{m,k} \times B_{k,n} \tag{12-16}\]

考虑三级结构的简单模型，寄存器/ cache/RAM，假设

cache足够大，同时放下$A_{m,k}$，$B_{k,n}$ 的$n_{r}$列$B_{j}$和$C_{m,n}$的$n_{r}$列$C_{j}$
$C_{j}+=AB_{j}$ 能全速利用CPU
$A_{m,k}$ 一直保留在cache里不会被切换出去

图12-17 gebp

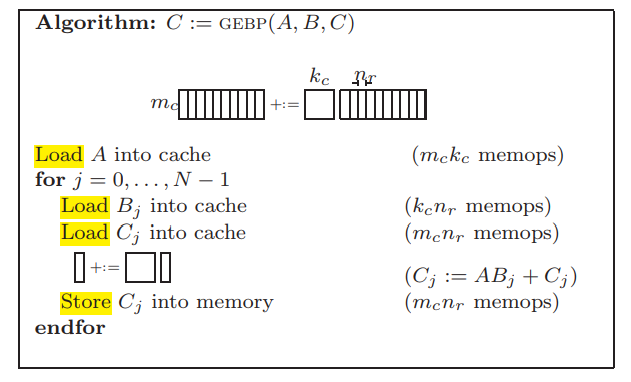
那么 - 把$A_{m,k}$整个放进cache的开销是$mk$， - 把$B_{k,n}$切分成$n_{r}$列一份，每次load进去一份开销是$kn_r$，一共$kn$ - 把$C_{m,n}$切分成$n_{r}$列一份，每次load进去一份开销是$mn_r$，一共$mn$ - 计算完，把$C_{m,n_r}$结果store回的开销是$mn_r$，一共$mn$ - 总的内存开销是$mk+kn+2mn$ - 总的计算开销是$2kmn$

计算密度近似为，

\[\frac{2kmn}{mk+kn+2mn}\approx \frac{2kmn}{kn+2mn}= \frac{2km}{k+2m} \quad where\quad m<<n \tag{12-17}\]

让计算密度最大的方法是

最大化$km$，尽可能选择最大尺寸的$A_{m,k}$，使得$A_{m,k}$能够放进cache
尽量使得$k==m$，也就是$A_{m,k}$接近方阵

回到矩阵乘加¹¹，核心思想就是分割，将大矩阵分割成小块或者长条来适配cache，让一次数据读取做尽可能多的运算，提高计算密度。

图12-18 gemm矩阵拆分

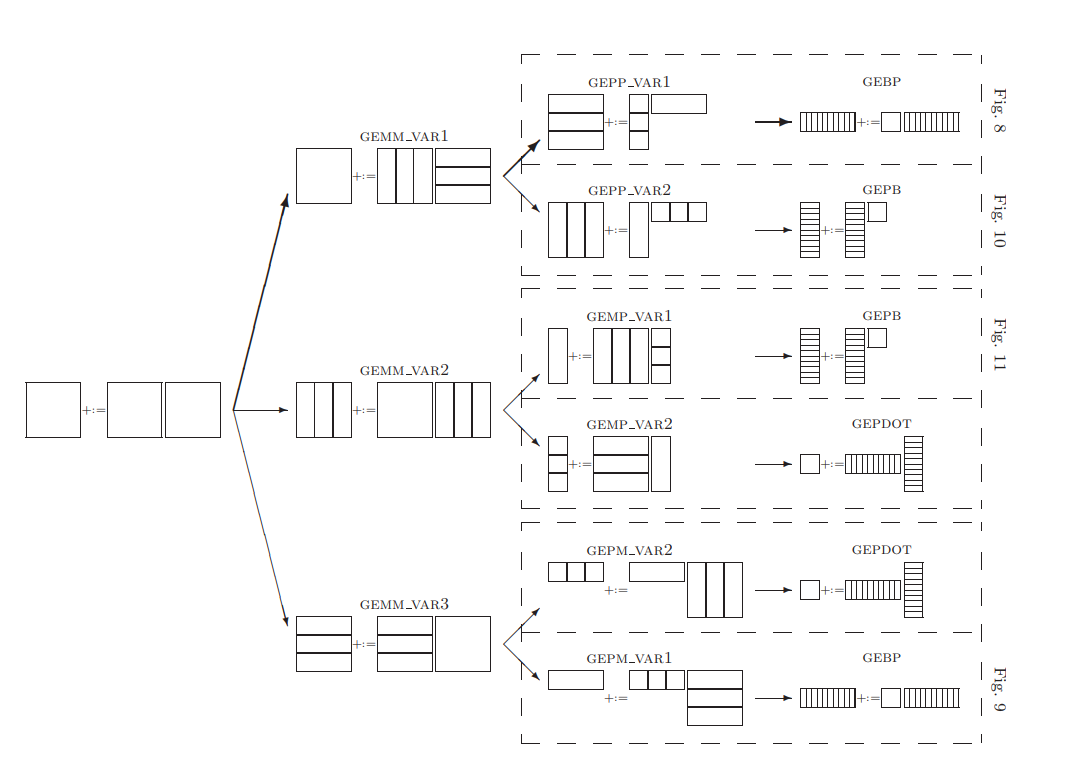
选择cache 当考虑更复杂一些的模型，带多级缓存。需要考虑把哪些数据缓存在L1 cache，哪些数据缓存在L2 cache。比如在VAR2中，分割直到的单元大小适配cache，然后再应用上面提到的GEBP/GEPB等方法
packing 当一个大矩阵乘法GEMM被拆分成GEBP时，会发生列数据不连续，直接方法会导致大量TLB miss，寻址不连续，这就需要额外的打包工作，将一个小矩阵打包到连续内存。

4.2.1 im2col

im2col有大神贾扬清实现在caffe，核心思想就是将卷积转换成GEMM - im2col转换，图像转换成矩阵 - GEMM计算

图12-19 im2col

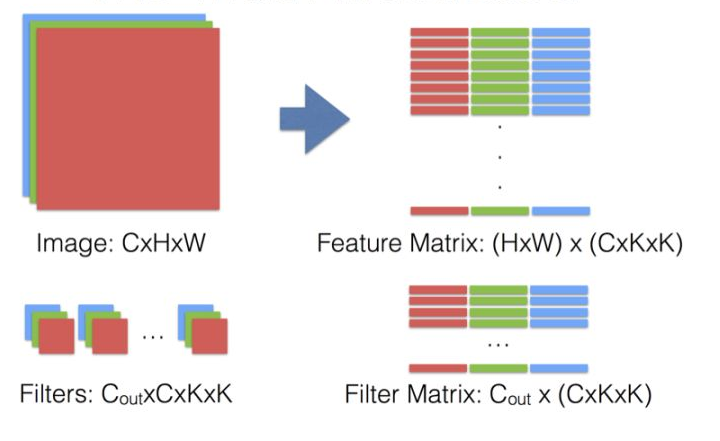
输入输出的$HW$不变，每一个输出的点都需要$C$个通道，每个通道$K\times K$的输入数据块。如之前所说，为了寻址的连续性，im2col方法预先将$C \times H\times W$的数据块连续排列。
卷积核也做了转置处理
这样卷积操作就转换成矩阵乘法操作，可以应用成熟的GEMM实现。 im2col的缺点就是内存开销增大，对于输入数据进行转换之后扩大了$k^2$倍

4.2.2 winograd/FFT

时域卷积可以转换成频域点乘，这两种方法本质上是，通过某种线性变换，把卷积核和输入变换到另一个域，FFT是频域，winograd是winograd域，原来空间域下的卷积在新的空间域下变成逐点相乘，再将点乘结果逆变换回原空间域¹²。

\[Y=A^T[(B^TdB)\bigodot (G^TgG)]A \tag{12-18}\]

性能比较

FFT不适合小卷积核，另外非常依赖FFT性能，设备端FFT通常只支持$2^n$的长度，对比卷积核的尺寸有要求
winograd适合小卷积核，比如$3\times3$卷积的的优化应用非常广，但是语音中用到的大量非方的卷积核和stride，不适合用winograd

4.2.3 低精度量化

在神经网络的训练阶段，最重要的是精度，其次才是速度，因此采用浮点表示是保证精度的最简单方法。但是在终端嵌入式设备上，天生地需要更小的内存占用，更快的运算速度，更低的功耗。这里将32bit浮点数量化成8bit定点数就非常有意义，当然是在维持统一水平的模型性能前提下。一个显而易见的好处就是模型占用空间缩小75%，然后8bit数据存取也会降低内存带宽，更高效地利用缓存，带来速度上的提升 ¹³¹⁴。量化过程中肯定会引入误差，从网络输入角度看，这些量化误差只是输入的噪声，网络应该有能力处理一定范围内的量化噪声，很多paper也实验证明了这一点。

将一个浮点数$r$，量化成定点数$q$，需要额外两个参数，缩放系数$s$和定标值$z$，$s$是浮点数，$Z$是定点数，公式如下

\[r = S(q-Z) \tag{12-19}\]

另外一种量化方式是先乘后减，这种量化方式已经被弃用，原因是浮点数0用这种方法量化之后有误差，而前一种方式中，定点数z就严格对于浮点数0。浮点数0会在pad中大量运用，因此现在都用前一种量化方式。考虑网络中最常见的矩阵乘法操作，三个浮点矩阵乘法，用量化方式表示，

\[r_3^{(i,k)}=\sum_{j=1}^N{r_1^{(i,j)}r_2^{(j,k)}} \tag{12-20}\] \[S_3(q_3^{(i,k)}-Z_3)=\sum_{j=1}^N{S_1(q_1^{(i,j)}-Z_1)S_2(q_2^{(j,k)}-Z_2)} \tag{12-21}\] \[q_3^{(i,k)}=Z_3+\frac{S_1S_2}{S_1}\sum_{j=1}^N{(q_1^{(i,j)}-Z_1)(q_2^{(j,k)}-Z_2)} \tag{12-22}\]

与原始浮点矩阵乘法相比，不仅仍然有$N^3次$乘法和次$N^3次$加法，还增加了次减$2N^3次$法，输出矩阵的每个点都要做$2N$次减法。通过把乘法展开，可以降低运算复杂度。这里对于输入矩阵的行列分别求和，运算复杂度从$N^3$降低到$N^2$，因此此时核心的运算量还是在两个定点矩阵的乘法上。

5 总结

本章首先介绍了语言唤醒任务及其应用和评价标准，算法流程基本可以分为3个部分，特征提取，打分模型和后处理模块。在特征提取章节详细介绍了应用最广的Fbank和MFCC方法，PCEN又在Fbank基础上做了改进，目的是减少特征值与语音响度相关性。随后在模型结构章节按照出现时间节点依次介绍了几种主流的打分模型结构，可以看到算法向着参数量越来越小，精度越来越高快速演进着。相比其他机器学习任务比如人脸识别和物体检测，语言唤醒任务通常对于算力和内存开销有着更大的限制，除了从算法上做出优化改进之外，工程化方面也有很多优化的方向。在最后一张中介绍了几种工程化方面的加速手段，事实上这些方法不仅仅局限于语音唤醒任务，也同时适用于语言信号处理或者机器视觉任务等其他领域。安卓平台基于谷歌唤醒的代码以及工程见https://github.com/shichaog/tensorflow-android-speech-kws，里面有一个已经编译好的apk，手机开启开发者权限后adb install 后就可以使用了。

abbreviation

TPR (True Positive Rate)：召回率

FPR (False Positive Rate)：虚警率

LVCSR (Large Vocabulary Continuous Speech Recognition)：大词汇量连续语音识别

HMM (Hidden Markov Model)：隐马尔科夫模型

Fbank (Filter bank)：滤波器组

MFCC (Mel-Frequency Cepstral Coefficient)：Mel倒谱系数

STFT (Short-Time Fourier Transform)：短时傅里叶变换

DCT (Discrete Cosine Transform)：离散余弦变换

FFT (Fast Fourier Transform)：快速傅里叶变换

PCEN (Per-Channel Energy Normalization)：分通道能量归一化

AGC (Automatic Gain Control)：自动增益调整

DNN (Deep Neural Network)：深度神经网络

GMM (Gaussian Mixture Model)：高斯混合模型

ReLU (Rectified Linear Unit)：线性整流函数

CNN (Convolutional Neural Network)：卷积神经网络

RNN (Recurrent Neural Network)：循环神经网络

CTC (Connectionist Temporal Classification)

DSCNN (Depthwise Separable Convolution)

LSTM (Long Short-Term Memory)：长短期记忆网络

GRU (Gated Recurrent Unit)：门控循环单元

FLOP (FLoating-point OPerations)：浮点运算操作

GEMM (General Matrix to Matrix Multiplication)：通用矩阵和矩阵乘法

im2col (image to column)

参考文献

J.R. Rohlicek, W. Russell, S. Roukos, and H. Gish, “Continuous hidden Markov modeling for speaker-independent wordspotting,” in IEEE Proceedings of the International Conference on Acoustics, Speech and Signal Processing, 1990, pp. 627–630. ↩
Y. Wang, P. Getreuer, T. Hughes, R. F. Lyon, and R. A. Saurous, “Trainable frontend for robust and far-field keyword spotting,” arXiv preprint, arXiv:1607.05666, 2016. ↩
G. Chen, C. Parada, and G. Heigold, “Small-footprint keyword spotting using deep neural networks,” in Proceedings International Conference on Acoustics, Speech, and Signal Processing, 2014, pp. 4087-4091. ↩
T. N. Sainath and C. Parada, “Convolutional neural networks for small-footprint keyword spotting,” in Proceedings of Interspeech,2015, pp. 1478-1482 ↩
S. O. Arik, M. Kliegl, R. Child, J. Hestness, A. Gibiansky, et al, “Convolutional Recurrent Neural Networks for Small-Footprint Keyword Spotting,” INTERSPEECH, pp.1606-1610, 2017. ↩
François Chollet. Xception: Deep learning with depthwise separable convolutions. arXiv preprint arXiv:1610.02357, 2016. ↩
Xiangyu Zhang, Xinyu Zhou, Mengxiao Lin, and Jian Sun. Shufflenet: An extremely efficient convolutional neural network for mobile devices. arXiv preprint arXiv:1707.01083, 2017. ↩
Yundong Zhang, Naveen Suda, Liangzhen Lai, and Vikas Chandra, “Hello edge: Keyword spotting on microcontrollers,” CoRR, 2017 ↩
Chieh-Chi Kao, Ming Sun, Yixin Gao, Shiv Vitaladevuni, Chao Wang. Sub-band Convolutional Neural Networks for Small-footprint Spoken Term Classification. arXiv preprint arXiv:1907.01448, 2019. ↩
Haitong Zhang, Junbo Zhang, Yujun Wang. Sequence-to-sequence Models for Small-Footprint Keyword Spotting. arXiv preprint arXiv:1811.00348, 2018. ↩
Kazushige Goto, Robert A. van de Geijn. Anatomy of high-performance matrix multiplication. ACM Transactions on Mathematical Software (TOMS). Volume 34 Issue 3, May 2008, Article No. 12. ↩
A. Lavin and S. Gray, “Fast algorithms for convolutional neural networks,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, pp. 4013–4021. ↩
B. Jacob, S. Kligys, Bo Chen, M. Zhu, M. Tang, A. Howard, H.Adam, D. Kalenichenko, “Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference,” IEEE Conference on Computer Vision and Pattern Recognition (CVPR), June 2018. ↩
Raghuraman Krishnamoorthi. Quantizing deep convolutional networks for efficient inference: A whitepaper. CoRR, abs/1806.08342, 2018. ↩