原文

Part 1: Introduction

定义学习问题

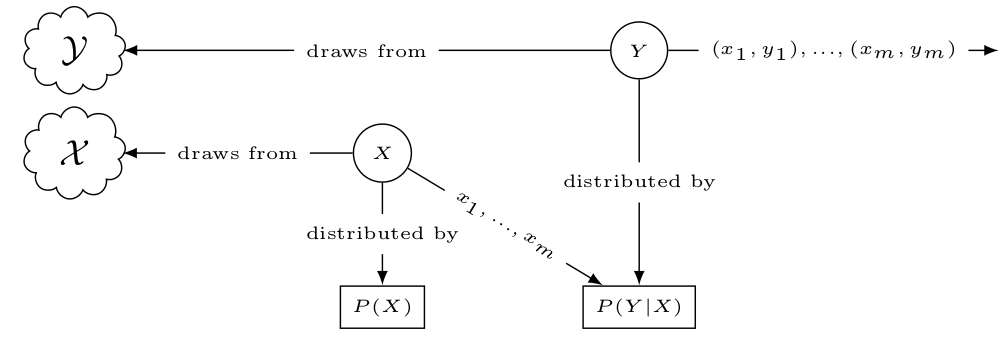
一个监督学习问题里，有一个观察到的数据集$S={(x_1,y_1), …, (x_m,y_m)}$，其中$x_i$是特征向量，$y_i$是label，学习目的是如何从给定$x_i$推断出$y_i$。已知条件

样本$(x_i, y_i)$是从一个更大集里随机采样出来的，正式表达为，两个随机变量$X$和$Y$分别遵循概率分布$P_X$和$P_Y$，$x$和$y$是这两个随机变量随机出来的数值。
特征和label之间存在关联，正式表达为，$Y$是$X$的条件概率$P(Y\vert X)=P(X)P(Y\vert X)$

可以定义一个统计模型来表达学习问题里条件概率分布关系

目标函数

我们不想直接和条件概率分布打交道，因此引入目标函数。用目标函数来简化代替条件概率函数。均值和方差可以用来分解一个随机变量，假设有两个随机变量$V$和$W$，

\[V=E[V\vert W]+(V−E[V\vert W])\]

$E[V|W]$是随机变量$V$和$W$的条件均值，上式说明随机变量$V$可以被分解成两部分

由另一个随机变量$W$表达部分
不能由另一个随机变量 $W$ 表达的随机部分， $Z=V−E[V\vert W]$ ，由全期望公式可知，这部分均值为 $0$， $E(Z)=E(V−E[V\vert W])=E(V)−E(V)=0$ ，因此这部分只包含方差，就是随机变量 $V$ 中不能被随机变量 $W$ 表达的方差 $\xi$

全期望公式 $E(E[V\vert W])=E(X)$

考虑一对随机变量$X$和$Y$随机出来的值$(x_i, y_i )$

\[y_i=E[Y\vert X=x_i ]+\xi\]

$\xi$是随机变量$Y$中不能被随机变量$X$表达的方差，称为noise项。

定义函数表示条件期望conditional expectation，将输入空间$X$映射到输出空间$Y$，$X\to Y$，$f(x)$称为目标函数，机器学习任务简化成估计函数$f$

\[E[Y\vert X=x]=f(x)\]

那么输入特征和输出label的条件概率表达$P(Y\vert X)$可以重写成

\[y=f(x)+\xi\]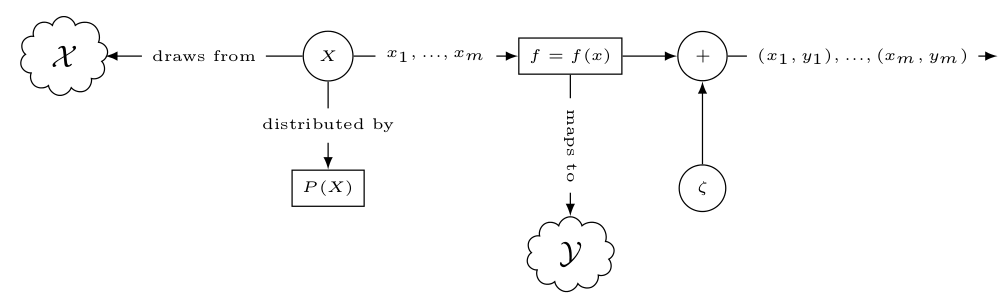

Hypothesis 假设目标函数

在估计目标函数的过程中，因为不能穷举所有函数，我们试图对于目标函数$f(x$)的形式做一个假设hypothesis。

假设目标函数是一个线性函数，或者球面非线性函数，无论做什么假设，都定义一个可能的目标函数空间称为hypothesis set。

比如，我们假设目标函数的形式是$ax+b$，那么hypothesis set $H$就是

\[H={h:x\to y\vert h(x)=ax+b}\]

函数$h(x)=3.2x−1$就是这个hypothesis set $H$里的一个具体实例

机器学习任务变成，从hypothesis set $H$里挑选一个实例目标函数$h$，使得实例目标函数$h$能最接近目标函数$f$。接下来的问题是，如何评估一个hypothesis目标函数接近目标函数？

损失函数

在整个数据集应用hypothesis函数$h$，然后求loss的均值，称为in-sample error或者the empirical risk

\[R_{emp}(h)=\frac{1}{m} \sum_{i=1}^m{L(y_i,hx_i)}\]

之所以被称为实验性的，是因为这个值来源于数据集中采样出来的实验数据。

The Generalization Error 泛化误差

学习的目标是数据集的概率分布，而不是数据集本身。

这就意味着hypothesis应该在没见过的采样数据上有小误差，在整个概率分布上定义泛化误差

\[R(h)=E_{((x,y)\sim P(X,Y))}[L(y_i,h(x_i))]\]

那么问题是，我们不知道这个联合分布$P(X,Y)$，也就没法计算这个泛化误差$R(h)$

Is the Learning Problem Solvable?

$R_{emp}(h)$是基于采样数据集的实验误差，$R(h)$是基于整个联合分布$P(X,Y)$的泛化误差，如何在数学上表示两者接近？

两者差值大于一个非常小值的概率足够小

\[P[sup_{h\in H}\vert R(h)−R_{emp}(h)\vert >\epsilon]\]

$R(h)$和$R_{emp}(h)$的差值绝对值的上确界 $sup_{h\in H}$，大于一个非常小值$\epsilon$的概率。如果这个概率足够小，说明$R(h$)和$R_{emp}(h$)的足够接近，那么这个学习问题是可解的。

上确界
一个实数集合A，若有一个实数M，使得A中任何数都不超过M，那么就称M是A的一个上界。在所有那些上界中如果有一个最小的上界，就称为A的上确界。

Part 2: Generalization Bounds

最小化empirical risk或者训练误差并不能解决学习问题，但是如果$R(h)$和$R_{emp}(h)$的差值足够小，学习问题就被被解决。

这里我们解释为什么这个差值可以做到很小。

Independently and Identically Distributed 独立同分布

首先做一个假设是，训练数据样本是独立同分布的 - inference的数据集是从同一个概率分布采样出来，满足同分布 - 采样的时候不依赖之前或之后的采样结果，样本之间没有依赖关系，满足样本之间相互独立

大数定律

当实验足够多次时，实验输出的平均值，接近真实分布的平均值，这称为大数定律。

有一随机变量$X$遵循概率分布$P$，从中采样出$m$个独立同分布的样本$x_1,x_2,…,x_m$，那么

\[\lim_{m\to \infty}⁡P[\vert E_{x\sim P}[X]−\frac{1}{m} \sum_{i=1}^m{x_i} \vert > \epsilon]=0⁡\]

这个版本称为弱大数定律，它保证当采样数足够大时，样本均值和真实均值足够接近，强大数定律版本是，样本均值就是真实均值。

应用到泛化误差上，对于某一个hypothesis函数$h$，只要样本数足够多，基于采样数据集的实验误差$R_{emp}(h)$和基于整个整个概率分布的$R(h)$泛化误差就足够接近

\[\lim_{m\to \infty}P[\vert R(h)−R_{emp}(h)\vert > \epsilon]=0\]

Hoeffding’s inequality 霍夫丁不等式

大数定律指示指引了原则性方向，但并没有提供任何方法，集中不等式Concentration inequality 提供了方法。

集中不等式描述了一个随机变量是否集中在某个取值附近:
- 马尔可夫不等式，从一个随机变量中采样出大于某特定值的概率上限
- 切比雪夫不等式，从一个随机变量中采样出小于某特定值的概率上限
- 霍夫丁不等式，从一个随机变量中采样出某个特定区间值的概率上限

有一随机变量$X$遵循概率分布$P$，从中采样出$m$个独立同分布的样本$x_1,x_2,…,x_m$，对于每个$a \leq x_i \leq b$，有

\[P[\vert E_{x\sim P}[X]−\frac{1}{m} \sum_{i=1}^m{x_i} \vert > \epsilon] \leq 2\exp{\frac{−2m\epsilon^2}{(b−a)^2}}\]

应用到泛化误差上，empirical risk定义是

\[R_{emp}(h)=\frac{1}{m} \sum_{i=1}^m{L(y_i,hx_i)}\]

式子$P[\vert E_{x\sim P}[X]−\frac{1}{m} \sum_{i=1}^m{x_i} \vert > \epsilon]$里的$x_i$实际上是测试集误差$L(y_i,hx_i)$，假设测试集误差$L(y_i,hx_i)$被限定在0和1之间，那么$b−a=1$

\[P[\vert R(h)−R_{emp}(h)\vert > \epsilon] \leq 2e^{−2m\epsilon^2}\]

其中$m$是样本数，意味着，随着样本数$m$增大，泛化误差指数下降。

这里的公式都是基于给定hypothesis函数 $h$前提下得到，而学习过程中并不知道hypothesis函数，需要从整个hypothesis空间里找一个。

因此我们需要一个泛化边界来反映挑选正确hypothesis函数的过程。

Generalization Bound: 1st Attempt

保证整个hypothesis空间都满足泛化误差不超过$\epsilon$，表达式可以重写成

\[P[sup_{h\in H}⁡ \vert R(h)−R_{emp}(h) \vert > \epsilon]=P[\bigcup_{h\in H}⁡ \vert R(h)−R_{emp}(h)\vert > \epsilon]\]

$\bigcup$表示或运算，也就是，对于hypothesis集$H$里的每一个hypothesis函数$h$，都满足泛化误差足够小概率

应用布尔不等式得到

\[P[\bigcup_{h\in H}⁡ \vert R(h)−R_{emp}(h)\vert > \epsilon] \leq \sum_{h\in H} P[\vert R(h)−R_{emp}(h)\vert > \epsilon]\]

布尔不等式数学归纳法

\[\because P(A\bigcap B)\geq0 \\ \therefore P(A\bigcup B)=P(A)+P(B)-P(A\bigcap B)\leq P(A)+P(B)\]

应用霍夫丁不等式得到

\[\sum_{h\in H} P[\vert R(h)−R_{emp}(h)\vert > \epsilon] \leq \sum_{h\in H}2 e^{−2m\epsilon^2}=2\vert H \vert e^{−2m\epsilon^2} \\\]

$\vert H \vert$是hypothesis空间的尺寸，hypothesis函数数目

最终得到，整个hypothesis空间都满足泛化误差不超过$\epsilon$的概率上限

\[P[sup_{h\in H}⁡ \vert R(h)−R_{emp}(h) \vert > \epsilon] \leq 2\vert H \vert e^{−2m\epsilon^2} \\\]

令

\[2\vert H\vert e^{−2m\epsilon^2}=\sigma \\ \epsilon=(\frac{\ln \vert H\vert + \ln \frac{2}{\sigma}}{2m})^\frac{1}{2} \\ m=\frac{1}{2\epsilon^2}(\ln{\vert H\vert}-\ln{\sigma})\]

那么给定泛化误差小值$\epsilon$，得到$\sigma=2\vert H\vert e^{−2m\epsilon^2 }$

\[R(h)−R_{emp}(h)\leq \epsilon \\ R(h)−R_{emp}(h)\leq (\frac{\ln \vert H\vert + \ln \frac{2}{\sigma}}{2m})^\frac{1}{2} \\ R(h)\leq R_{emp}(h) + (\frac{\ln \vert H\vert + \ln \frac{2}{\sigma}}{2m})^\frac{1}{2}\]

由$\epsilon=(\frac{\ln \vert H\vert + \ln \frac{2}{\sigma}}{2m})^\frac{1}{2}$可见

hypothesis空间$\vert H\vert $越大，泛化误差$\epsilon$越大。

由$m=\frac{1}{2\epsilon^2}(\ln{\vert H\vert}-\ln{\sigma})$可见

在给定泛化误差$\epsilon$前提下，hypothesis空间$\vert H\vert $越大，所需要的训练集样本数$m$越大

在给定hypothesis空间$\vert H\vert $前提下，随着训练集样本数$m$变大，泛化误差$\epsilon$变小收敛至0，收敛速度是$O(\frac{1}{m})$

下面分别讨论一一对应方法和线性hypoth空间两种例子

一一对应方法

把训练集的特征和label做一个表一一对应记下来，那么在 - 数据集上的误差是0 $R_{emp}(h)=0$ - hypothesis空间$\vert H\vert $无穷大，因为hypothesis空间大小和样本空间大小一样，$(\frac{\ln \vert H\vert + \ln \frac{2}{\sigma}}{2m})^\frac{1}{2}=\infty$

所以这种方法的泛化误差是无穷大。

线性hypothesis空间

hypothesis空间$h(x)=ax+b$，因为$a$和$b$可以取无穷多个值，那么这个空间的$\vert H\vert$也是无穷大，与一一对应的方法泛化误差是一样的，那ML还有意义？

按照不等式$P[\bigcup_{h\in H}⁡ \vert R(h)−R_{emp}(h)\vert > \epsilon] \leq \sum_{h\in H} P[\vert R(h)−R_{emp}(h)\vert > \epsilon]$的上限$\sum_{h\in H} P[\vert R(h)−R_{emp}(h)\vert > \epsilon]$看，是的，线性hypothesis和一一对应方法一样没有任何意义，泛化误差无穷大。但是当这个不等式取到上限值时，意味着表示hypothsis空间内的所有的函数都是独立不相关的。

布尔不等式数学归纳法，当$P(A\bigcap B)=0$时，才会出现上限值$P(A\bigcup B)=P(A)+P(B)-P(A\bigcap B)=P(A)+P(B)$

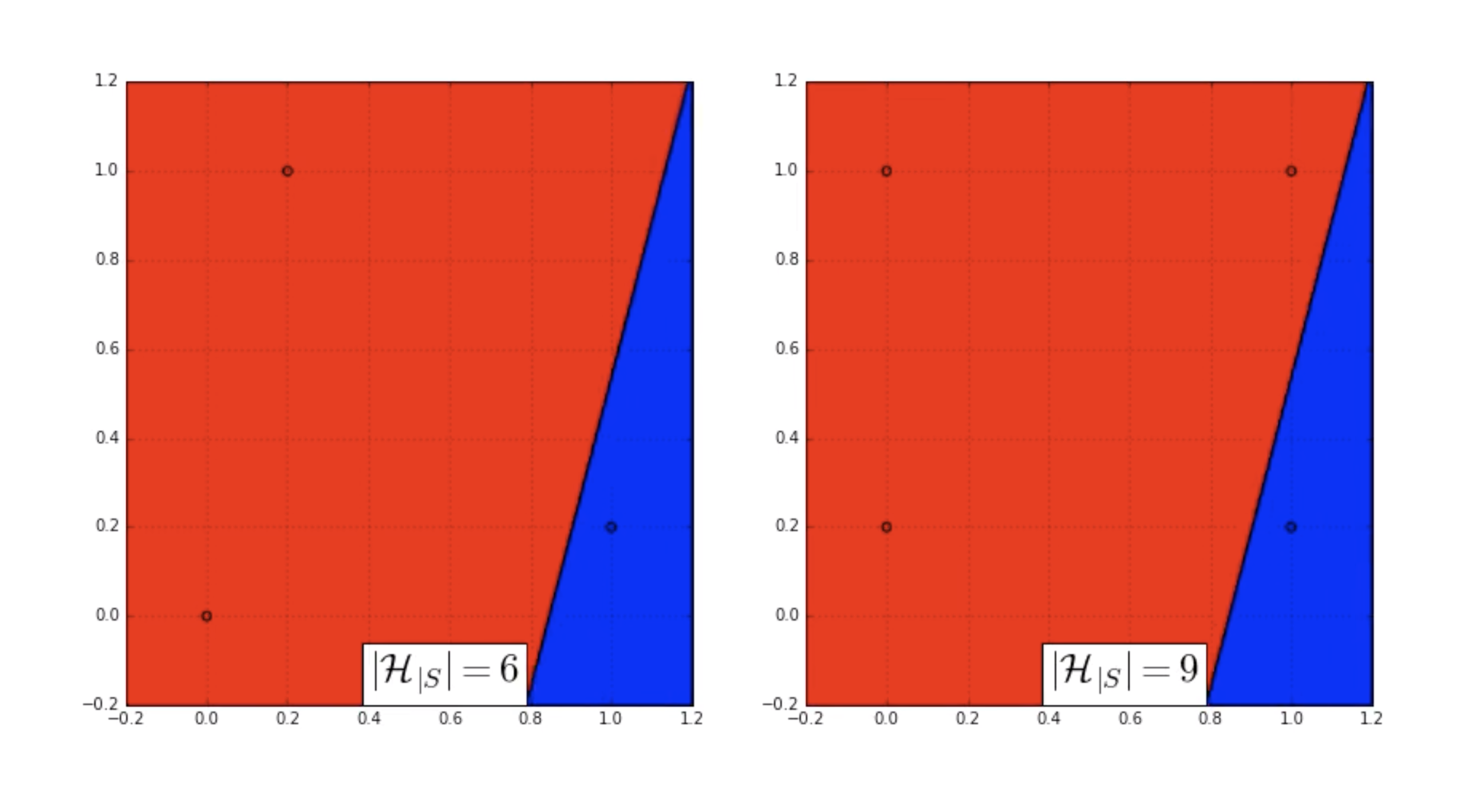
而实际中hypothsis空间内的函数都是相关的，那么上面的不等式并不可能取到上限值。也就是说，对于两个hypothesis $h_1, h_2\in H$，事件$\vert R(h_1)−R_{emp}(h_1 )\vert >\epsilon $和事件$\vert R(h_2)−R_{emp}(h_2)\vert >\epsilon $不是独立的，这一点成立么？

检查独立性假设

上图给出一个例子说明，在给定线性hypothesis集和数据集下， $h_1, h_2\in H$，事件$\vert R(h_1)−R_{emp}(h_1 )\vert >\epsilon $和事件$\vert R(h_2)−R_{emp}(h_2)\vert >\epsilon $不是独立的。

比如上面图中，如果红色hypothesis有较大泛化误差，那么相同斜率红色上方的所有hypothesis都有较大误差，图上所有的线性hypothesis都是有相关性的，连带着对应的泛化误差时间也是相关的。

既然两个事件不是独立的，那么$\sum_{h\in H} P[\vert R(h)−R_{emp}(h)\vert > \epsilon]$这个上限值太宽松了，太消极悲观了。我们得找一个更合适的上限值。

The Symmetrization Lemma 对称引理

假设我们还有一个尺寸为m的ghost数据集$S′$，可以证明，待证明

\[P[sup_{h\in H}⁡ \vert R(h)−R_{emp}(h) \vert > \epsilon] \leq 2*P[sup_{h\in H}⁡ \vert R(h)−R'_{emp}(h) \vert > \frac{\epsilon}{2}]\]

$R’_{emp}(h)$是hypothesis $h$在ghost数据集$S′$上得到的实验误差，这个式子说明（数据集S的最大实验泛化误差 - 真实泛化误差）大于$\epsilon$的概率，是（数据集S的最大实验泛化误差 - 数据集S’的最大实验泛化误差）大于$\frac{\epsilon}{2}$的概率的两倍

这样的好处是，不等式右边不存在真实泛化误差，都用实验泛化误差来表示边界上限，因此不需要考虑整个输入输出空间。 这种方法被称为 symmetrization lemma, was one of the two key parts in the work of Vapnik-Chervonenkis (1971).

The Growth Function

看到在一个数据集中，许多hypothesis函数都对应相同的empirical risk，从中选择一个hypothesis称为有效hypothesis。有效hypothesis空间是原hypothesis空间的一个子集，而且依赖于数据集，我们标记为$H_\vert S$

有效hypothesis空间$H_\vert S$是一个，和数据集，hypothesis空间和模型算法复杂度相关的变量，理论上模型算法越复杂，$H_\vert S$可能越大。

那么根据Generalization Bound: 1st Attempt中得到的结论 $P[sup_{h\in H}⁡ \vert R(h)−R_{emp}(h) \vert > \epsilon] = P[\bigcup_{h\in H}⁡ \vert R(h)−R_{emp}(h)\vert > \epsilon] \\ \leq \sum_{h\in H} P[\vert R(h)−R_{emp}(h)\vert > \epsilon] \\ = \vert H \vert P[\vert R(h)−R_{emp}(h)\vert > \epsilon]$

可以得到

\[P[sup_{h\in H_{\vert S \bigcup s'}}⁡ \vert R_{emp}(h)−R'_{emp}(h) \vert > \frac{\epsilon}{2}] \leq \vert H_{\vert S \bigcup s'} \vert P[\vert R_{emp}(h)−R'_{emp}(h) \vert > \frac{\epsilon}{2}]\]

因为这里同时用数据集$S$和$S′$，所以hypothesis空间被限定在$S\bigcup S′$，那么现在被限定的hypothesis空间的大小是多少？$\vert H_\vert S\bigcup S′ \vert=?$ 限定的hypothesis空间的大小就是，value/label空间$S\bigcup S′$提取的独立元素个数比如考虑二分类问题，label $y={−1, +1}$，数据集中包含$m$个样本，从这个空间能提取的sample数（value, label）对数是，distinct labellings就是$2^m$

这里有效sample数不是$2m$，而是$2^m$，比如$m=3$情况下，假设$y={−1, +1}, x={−1, 0, +1}$，每个样本都有都有两种可能，$(x,−1)$和$(x,+1)$，那么3个样本张成的空间有$2^3=8$种可能

CASE	SAMPLE#1 #2 #3
1	1,1,1
2	1,1,-1
3	1,-1,1
4	-1,1,1
5	-1,-1,1
6	1,-1,-1
7	-1,1,-1
8	-1,-1,-1

给定一个大小是m的数据集$S$，对应hypothesis空间是$H$，用$\Delta_H (m)$ grouth function表示这种情况下的有效sample数目，也就是被个大小是m的数据集S限制的hypothesis空间大小$\Delta_H (m)=\vert H_{\vert S }\vert$

\[P[sup_{h\in H_{\vert S \bigcup s'}}⁡ \vert R_{emp}(h)−R'_{emp}(h) \vert > \frac{\epsilon}{2}] \leq \Delta_{H_{\vert S \bigcup s'}}(2m) P[\vert R_{emp}(h)−R'_{emp}(h) \vert > \frac{\epsilon}{2}]\]

因为这里用了两个训练集，每个训练集大小是$m$，合并之后的数据集$S \bigcup s’$，最坏情况下，两个数据集没有任何sample是重复的，因此合并数据集$S \bigcup s’$的大小就是$2m$，被合并数据集$S \bigcup s’$限制的hypoth空间大小根据grouth function定义就是$\Delta_{H_{\vert S \bigcup s’}}(2m)$

对于二分类问题$\Delta_H (m)\leq 2^m$，那么

\[\Delta_{H_{\vert S \bigcup s'}}(2m) \leq 2^{2m} \\ P[sup_{h\in H_{\vert S \bigcup s'}}⁡ \vert R_{emp}(h)−R'_{emp}(h) \vert > \frac{\epsilon}{2}] \leq 2^{2m} P[\vert R_{emp}(h)−R'_{emp}(h) \vert > \frac{\epsilon}{2}]\]

随着样本空间$m$增加，$2^{2m}$项增长得太快了，需要进一步限定

西瓜书

给定一个大小是$m$的数据集$S={x_1, x_2, …, x_m}$，对应hypothesis空间是$H$，每个hypothesis函数都能对$S$中的所有样本给出一个label集合，

\[h_{\vert S} = \{ h(x_1), h(x_2), ... , h(x_m) \}\]

随着$m$增大，这个label集合也会相应增大。定义，在个大小是$m$的数据集$S$上，hypothesis空间$H$的增长函数$\Delta_H (m)$为

\[\Delta_H(m) = \max_{\{ x_1, x_2, ..., x_m \}\in S}{\vert \{ (h(x_1), h(x_2), ... , h(x_m)) \vert h\in H\} \vert}\]

遍历hypothesis空间$H$里的所有hypothesis函数$h$，在数据集$S$上能给出的label集合的最大数目。增长函数$\Delta_H(m)$越大，表明hypothesis空间$H$在数据集$S$上能给出的label数越多，hypothesis空间$H$的表达能力越强，对学习任务的适应能力也越强。 因此增长函数$\Delta_H(m)$描述了hypothesis空间$H$在数据集$S$上的表达能力，反映了hypothesis空间$H$的复杂度。

The VC-Dimension

三点数据集的二分类问题

假设三个点是$abc$，理论上这个数据集可以提供有$2^3=8$种不同的sample组合，实际上线性hypothesis函数可以分出

\[(a), (b), (c), (a,b), (a,c), (b,c), (a,c,b), (NONE)\]

8种组合，和最大有效样本数一致

四点数据集的二分类问题

假设四个点从左到右从上到下是$abcd$，理论上这个数据集可以提供有$2^4=16$种不同的sample组合，实际上线性hypothesis函数分不出

\[(a,d), (b,c)\]

2种组合，实际只能分出$16-2=14$中组合，比最大有效样本数少

二分类任务里，数据集中包含$m$个样本，如果一个hypothesis空间的确能够产生所有$2^m$种有效样本，或者说，在这个数据集中能产生$m$种不同的empirical risk，我们称这个hypothesis空间打散了数据集。

实际上线性hypothesis不能打散任何4点数据集，比如下图

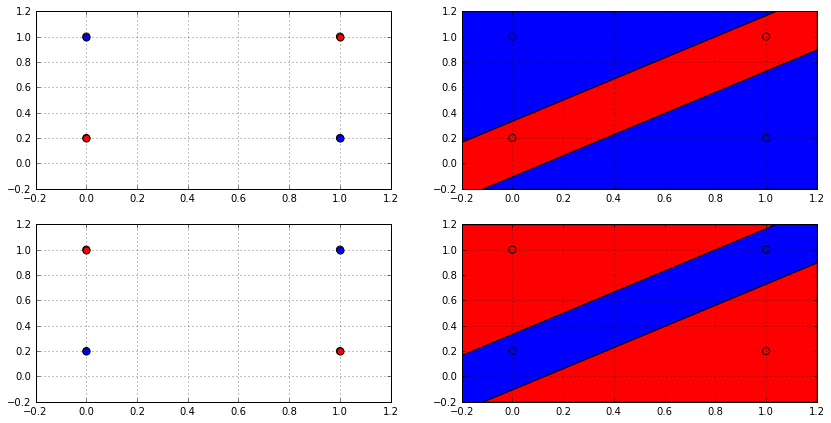
因此我们得到结论，hypothesis空间大小通常都不能达到样本空间大小，或者说hypothesis通常都不能打散样本空间。

如果一个hypothesis空间$H$最多只能分离尺寸是$k$的数据集，$m$是数据集样本总数，那么

\[\Delta_{H}(m) \leq \sum_{i=0}^{k}\begin{pmatrix}m\\i\end{pmatrix}\]

$\Delta_{H} (m)$ grouth function表示被样本数是$m$的数据集限制的hypothesis空间大小，或者说，样本数是$m$的数据集加上hypothesis空间所能提供的

最早由Vapnik-Chervonenkis提出，hypothesis空间$H$最多只能分离的数据集大小$k$，被称为$H$的VC-dimension $d_{vc}$
同时这个理论独立被Norbert Sauer证明，因此也被称为Sauer’s lemma

2D线性分类器，$d_{vc}=3$
$R^n$空间内的超平面hyperplane分类器$d_{vc}=n+1$

应用Sauer’s lemma可以进一步减小上边界，进一步推导，待证明

\[\Delta_{H}(m) \leq \sum_{i=0}^{k}\begin{pmatrix}m\\i\end{pmatrix} \leq (\frac{m.e}{d_{vc}})^{d_{vc}} \leq O(m^{d_{dv}}) \\ \begin{pmatrix}m\\i\end{pmatrix} = \frac{m\cdot (m-1)\cdot ... \cdot (m-i+1)}{i!}\]

这里O是大O符号（Big O notation）是用于描述函数渐进行为的数学符号。更确切地说，它是用另一个（通常更简单的）函数来描述一个函数数量级的渐近上界。 $d_{vc}$可以用来衡量hypothesis空间的复杂度或者丰富程度

相比于之前的上边界$2^{2m}$，$O(m^{d_{vc}})$已经不再是指数增长了，边界被缩小了。

西瓜书

打散定义

hypothesis空间$H$在数据集$S$上能给出的label最大数目为增长函数$\Delta_H(m)$，假设这是一个二分类任务，样本数为$m$的数据集$S$最大只可能出现$2^m$种label，如果

\[\Delta_H(m)=2^m\]

那么我们称数据集$S$被hypothesis空间$H$打散。

VC维定义

hypothesis空间$H$的VC维定义是，能被$H$打散的最大数据集大小，比如二分类里

\[d_{VS}(H)=\max\{m: \Delta_H(m)=2^m\}\]

$d_{VS}(H)=d$表明，存在大小为$d$的数据集可以被hypothesis空间$H$打散，而且这和数据集的数据分布无关。注意，这不意味着所有大小为$d$的数据集都可以被hypothesis空间$H$打散。 举例，上文中的线性hypothesis可以打散3点数据集，但不能打散任何4点数据集，所以线性hypothesis的VC维为3。

Sauer’s lemma

Sauer引理给出VC维和增长函数之间的定量关系，假设hypothesis空间$H$的VC维是$d$

\[\Delta_{H}(m) \leq \sum_{i=0}^{d}\begin{pmatrix}m\\i\end{pmatrix}\]

数学归纳法证明可证明，见书未证明。

由上面的公式可以推导增长函数的上限

\[\Delta_{H}(m) \leq (\frac{e\cdot m}{d})^{d}\]

基础1，假设数据集大小$m$远大于VS维$d$

\[m>d \\ (\frac{m}{d})^{d-i} > 1\]

基础2，二项式级数展开公式

\[(1+x)^m = \sum_{i=0}^{\infty}\begin{pmatrix}m\\i\end{pmatrix} x^{i} \geq \sum_{i=0}^{d}\begin{pmatrix}m\\i\end{pmatrix} x^{i}\]

基础3，洛必达法则，夹逼定理可证明

\[\lim_{x->\infty}{(1+x)^{\frac{1}{x}}}=e \\ \lim_{x->\infty}{\ln{(1+x)^{\frac{1}{x}}}}=1\]

可以证明

\[\Delta_{H}(m) \leq \sum_{i=0}^{d}\begin{pmatrix}m\\i\end{pmatrix} \\ \leq \sum_{i=0}^{d}\begin{pmatrix}m\\i\end{pmatrix} (\frac{m}{d})^{d-i}\\ = (\frac{m}{d})^{d}\sum_{i=0}^{d}\begin{pmatrix}m\\i\end{pmatrix} (\frac{d}{m})^{i}\\ \leq (\frac{m}{d})^{d}\sum_{i=0}^{m}\begin{pmatrix}m\\i\end{pmatrix} (\frac{d}{m})^{i} \\ \leq (\frac{m}{d})^{d}\sum_{i=0}^{\infty}\begin{pmatrix}m\\i\end{pmatrix} (\frac{d}{m})^{i} \\ = (\frac{m}{d})^{d}(1+\frac{d}{m})^m \\ = (\frac{m}{d} (1+\frac{d}{m})^\frac{m}{d})^d \\ \leq (\frac{e\cdot m}{d})^d\]

The VC Generalization Bound

讨论，整个hypothesis空间都满足泛化误差不超过$\epsilon$的概率，表示为$P[sup_{h\in H}⁡ \vert R(h)−R_{emp}(h) \vert > \epsilon] $ 在Generalization Bound: 1st Attempt里，单纯应用Hoeffding’s inequality 霍夫丁不等式可以得到

\[P[sup_{h\in H}⁡ \vert R(h)−R_{emp}(h) \vert > \epsilon] \leq 2\vert H \vert e^{−2m\epsilon^2} \\\]

令 $\sigma=2\vert H\vert e^{−2m\epsilon^2}$有

\[\epsilon=(\frac{\ln \vert H\vert + \ln \frac{2}{\sigma}}{2m})^\frac{1}{2}\]

可以得到泛化误差的上限

\[R(h) \leq R_{emp}(h) + \epsilon \\ = R_{emp}(h) + (\frac{\ln \vert H\vert + \ln \frac{2}{\sigma}}{2m})^\frac{1}{2}\]

在给定hypothesis空间$\vert H\vert $前提下，随着训练集样本数$m$变大，泛化误差$\epsilon$变小收敛至0，收敛速度是$O(\frac{1}{m})$。

Vapnik-Chervonenkis theory 可以利用增长函数来进一步缩小边界，进而增快收敛速度。增长函数$\Delta_H(m)$描述了hypothesis空间$H$在数据集$S$上的表达能力，反映了hypothesis空间$H$的复杂度。 Vapnik-Chervonenkis theory 定义证明了增长函数和泛化误差之间的关系 $P[sup_{h\in H}⁡ \vert R(h)−R_{emp}(h) \vert > \epsilon] \leq 4\Delta_H(2m) \exp(-\frac{m\epsilon^2}{8})$

令$\sigma = 4\Delta_H(2m) \exp(-\frac{m\epsilon^2}{8})$有

\[\epsilon = \sqrt{\frac{8\ln{\Delta_H(2m)}+8\ln{\frac{4}{\sigma}}}{m}}\]

可以得到泛化误差的上限

\[R(h) \leq R_{emp}(h)+\epsilon \\ =R_{emp}(h)+\sqrt{\frac{8\ln{\Delta_H(2m)}+8\ln{\frac{4}{\sigma}}}{m}}\]

代入上面得到的结论$\Delta_{H}(m) \leq (\frac{e\cdot m}{d})^{d}$得到

\[R(h)=R_{emp}(h)+\sqrt{\frac{8\ln{(\frac{e\cdot 2m}{d})^{d}}+8\ln{\frac{4}{\sigma}}}{m}} \\ =R_{emp}(h)+\sqrt{\frac{8d\ln{(\frac{2m}{d}+1)}+8\ln{\frac{4}{\sigma}}}{m}}\]

在给定hypothesis空间$\vert H\vert $前提下，随着训练集样本数$m$变大，泛化误差$\epsilon$变小收敛至0，收敛速度是$O(\frac{1}{\sqrt{m}})$。 VC定理将收敛速度从$O(\frac{1}{m})$提高到$O(\frac{1}{\sqrt{m}})$。

One Inequality to Rule Them All

这里讨论的VC边界只适用于二分类问题，但是VC概念框架，包括打散，增长函数和VC维度，同样可以推广到多分类和回归问题。 Natarajan维度是VC维度在多分类问题上的推广，pseudo维度是VS维度在回归问题上的推广。还有Rademacher复杂度，通过hypothesis空间对于随机噪声的适应性来评估hypothesis空间的丰富程度。Rademacher复杂度可以适用任何学习问题。不管用什么工具，泛化误差边界都可以表示成

\[R(h)=R_{emp}(h)+C(\vert H \vert, N, \sigma)\]

这里$C$是hypothesis空间复杂度/大小/丰富程度，$N$是数据集大小，$1-\sigma$是关于这个边界的置信度。这个公式说明，泛化误差可以有两方面组成，实验误差和模型复杂度。

Part 3: Regularization and the Bias-variance Trade-off

上面得到泛化误差的结论

\[R(h)=R_{emp}(h)+C(\vert H \vert, N, \sigma)\]

假设训练集$N$和置信度$\sigma$固定，进一步简化为

\[R(h)=R_{emp}(h)+C(\vert H \vert)\]

后面的讨论都会基于这个简化公式。这个公式直觉上看，hypothesis空间应该越丰富，泛化误差越小，实际中不是这样。

Why rich hypotheses are bad?

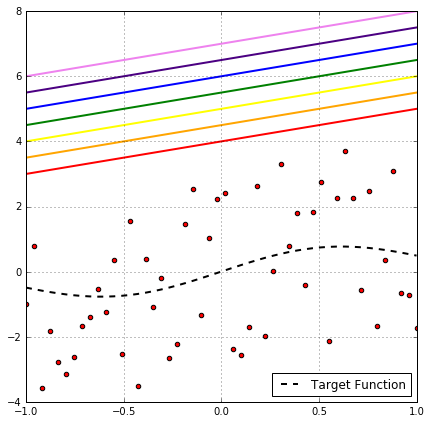
假设从区间$[-1, 1]$里均匀采样出样本$x$，目标函数为$f(x)=\sin(x)$，生成带噪信号$y=f(x)+\zeta$，这里$\zeta$是随机噪声，均值0方差2。在100个仿真数据集上，每个数据集200个点上分别训练三个hypothesis

线性hypothesis，$h(x)=w_1x+w_0$
立方hypothesis，$h(x)=w_1x+w_2x^2+w_3x^3+x_0$
10维多项式hypothesis

每个模型用浅蓝色曲线表示，100集平均的模型用深蓝色曲线表示，目标函数用黑色曲线表示。正常如果没有噪声的话，所有数据集点都在黑色曲线上，图中偏离目标函数黑色曲线的点都是带噪样本。距离越远，噪声越大。

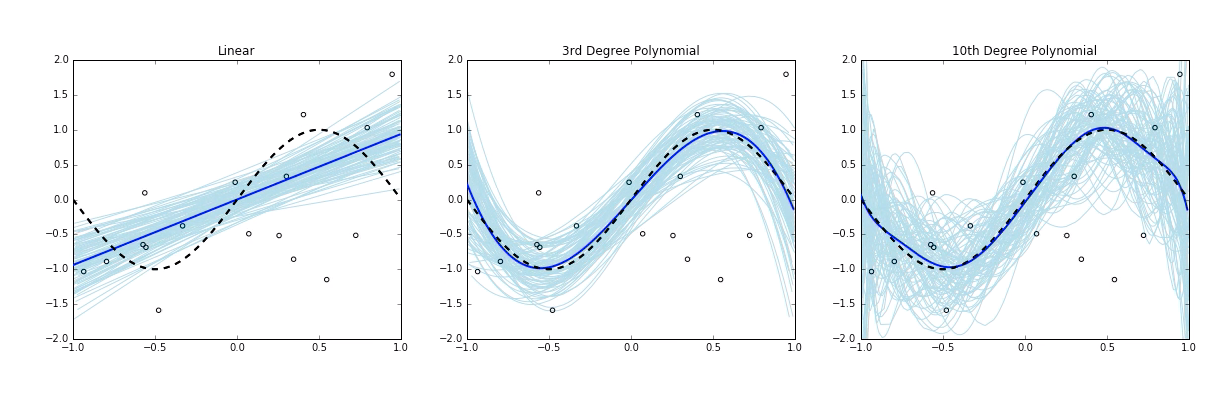
首先注意到，hypothesis越复杂越丰富，和目标函数的平均误差越小。 定义bias为期望输出和真实标记的差别

\[bias(x)=\overline{h}(x)-f(x)\]

其中$f(x)$是真实标记，$\overline{h}(x)$是期望输出，是不同训练集上训练的不同hypothesis得到的输出取平均，即$\overline{h}(x)=E_{D}[h^{(D)}(x)]$，$h^{(D)}(x)$表示训练集$D$上训练出来的hypothesis函数。将目标函数$f(x)=\sin(x)$用泰勒级数展开

\[\sin(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\frac{x^9}{9!}-...\]

随着分解的级数越来越大，高阶成分对函数值得影响也越来越小。

线性hypothesis，$h(x)=w_1x+w_0$可以拟合出$\sin(x)$的$x$项，但是从$x^3$往面就没法拟合。
立方hypothesis，$h(x)=w_1x+w_2x^2+w_3x^3+x_0$可以拟合出$x, x^3$项，从$x^4$往面就没法拟合。
10维多项式hypothesis，可以拟合出$x, x^3, x^5, x^7, x^9$项，从$x^11$往面就没法拟合。

10维多项式相比于立方函数，能减少的bias有限，因为立方函数不能拟合的$x^5, x^7, x^9$对于输出贡献有限。

其次注意到，hypothesis越复杂，hypothesis拟合噪声的能力越强。比如10维多项式函数可以拟合到图像顶部的，远远偏离目标函数的点，我们称这个hypothesis在这个带噪数据集里过拟合了。

量化过拟合 不同训练集上训练的不同hypothesis，相同输入$x$经过不同hypothesis得到$h(x)$之间的方差来量化过拟合程度 $var(x)=E_{D}[(h^{(D)}(x)-\overline{h}(x))^2]$

总结

hypothesis越复杂，和目标函数的平均误差越小
hypothesis越复杂，越容易过拟合

The Bias-variance Decomposition 偏差方差分解

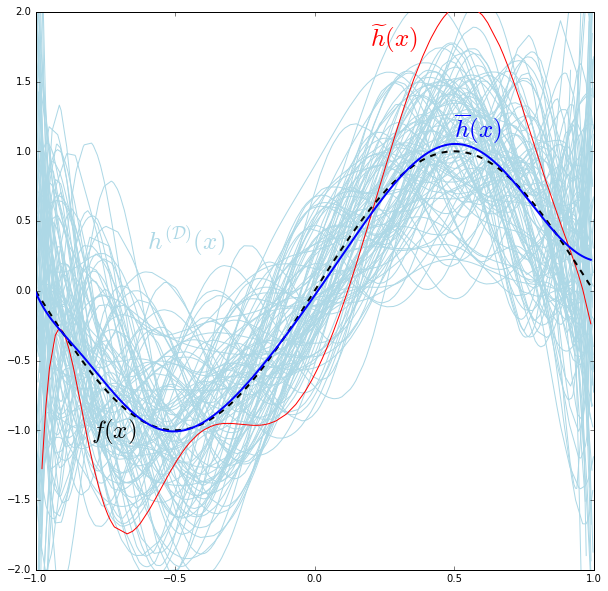
因为训练集$D$是随机从数据集中采样的，因此 $h^{(D)}(x)$也可以看作是随机变量。用part1中的trick，一个随机变量可以分解成两个成分，表达均值的确定成分和表达方差的随机部分

\[h^{(D)}(x)=\overline{h}(x)+H_{\sigma}^{(D)}(x)\]

其中$H_{\sigma}^{(D)}(x)$的均值是0，方差等于hypothesis的方差

\[Var(H_{\sigma}^{(D)}(x))=E_{D}[(h^{(D)}(x)-\overline{h}(x))^2]\]

用均方误差函数$L(\hat{y}, y)=(\hat{y}-y)^2$，可以定义在某一个采样点$x$出的误差Risk

\[R(h(x)) = E_{D}[L(h^{(D)}(x), f(x))] = E_{D}[(h^{(D)}(x)-f(x))^2]\]

代入$h^{(D)}(x)=\overline{h}(x)+H_{\sigma}^{(D)}(x)$和$bias(x)=\overline{h}(x)-f(x)$可得到

\[R(h(x)) = E_{D}[(\overline{h}(x)+H_{\sigma}^{(D)}(x)-f(x))^2] \\ = E_{D}[(bias(x)+H_{\sigma}^{(D)}(x))^2] \\ = E_{D}[(bias(x))^2+2bias(x)H_{\sigma}^{(D)}(x)+(H_{\sigma}^{(D)}(x))^2]\]

因为bias不依赖数据集$D$

\[R(h(x)) = (bias(x))^2 + 2bias(x)E_{D}[H_{\sigma}^{(D)}(x)] + E_{D}[(H_{\sigma}^{(D)}(x))^2]\]

因为$H_{\sigma}^{(D)}(x)$的定义就是均值为0，所以

\[Mean(H_{\sigma}^{(D)}(x))=E_{D}[H_{\sigma}^{(D)}(x)]=0 \\ Var(H_{\sigma}^{(D)}(x))=E_{D}[(H_{\sigma}^{(D)}(x)-Mean(H_{\sigma}^{(D)}(x)))^2]=E_{D}[(H_{\sigma}^{(D)}(x))^2]\]

那么有

\[R(h(x)) = (bias(x))^2 + E_{D}[(H_{\sigma}^{(D)}(x))^2] \\ = (bias(x))^2 + Var(H_{\sigma}^{(D)}(x)) \\ = (bias(x))^2 + E_{D}[(h^{(D)}(x)-\overline{h}(x))^2] \\ = (bias(x))^2 + var(x)\]

西瓜书

$h^{(D)}$表示训练集$D$上训练出来的hypothesis函数，$h^{(D)}(x)$是这个hypothesis函数在$x$点的预测输出。因为训练集$D$是随机从数据集中随机采样的，因此 $h^{(D)}(x)$也可以看作是随机变量。

偏差 bias bias定义为$h^{(D)}(x)$的期望$\overline{h}(x)=E_{D}[h^{(D)}(x)]$，和真实标记$f(x)$的偏离程度，反映算法本身的拟合能力

\[bias(x)=\overline{h}(x)-f(x)\]

方差 var var反映$h^{(D)}(x)$内部的波动情况，或者说偏离均值的程度，反映训练集波动导致的学习性能变化，数据扰动所造成的影响

\[var(x) = E_{D}[(h^{(D)}(x)-\overline{h}(x))^2]\]

噪声 噪声反映真实标记和数据集中的标记的偏离

\[\epsilon^2 = E_{D}[(y_D-y)^2]\]

用均差误差函数作为loss函数，预测输出为$h^{(D)}(x)$，真实label为$y$，数据集实际label为$y_D$，期望的泛化误差可以分解成偏差，方差和噪声之和。

\[E_{D}[(h^{(D)}(x)-y_D)^2] = E_{D}[(h^{(D)}(x)-\overline{h}(x)+\overline{h}(x)-y_D)^2] \\ = E_{D}[(h^{(D)}(x)-\overline{h}(x))^2] + E_{D}[(\overline{h}(x)-y_D)^2] + E_{D}[2(h^{(D)}(x)-\overline{h}(x))(\overline{h}(x)-y_D)] \\ \quad \\ \because \overline{h}(x)=E_{D}[h^{(D)}(x)] \\ \therefore E_{D}[2(h^{(D)}(x)-\overline{h}(x)]=E_{D}[2(h^{(D)}(x)]-\overline{h}(x)=0 \\ \quad \\ = E_{D}[(h^{(D)}(x)-\overline{h}(x))^2] + E_{D}[(\overline{h}(x)-y_D)^2] \\ = var(x) + E_{D}[(\overline{h}(x)-y+y-y_D)^2] \\ = var(x) + E_{D}[(\overline{h}(x)-y)^2] + E_{D}[(y-y_D)^2] + E_{D}[2(\overline{h}(x)-y)(y-y_D)] \\ \quad \\ \text{assume}\qquad E_{D}[y-y_D]=0 \quad \\ = var(x) + E_{D}[(\overline{h}(x)-y)^2] + E_{D}[(y-y_D)^2] \\ = var(x) + (bias(x))^2 + \epsilon^2\]

一般来说bias和var是冲突的，称为Bias–variance tradeoff。

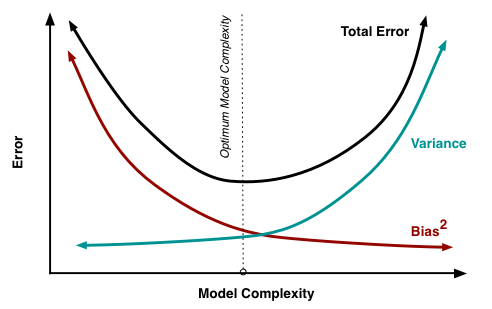
给定学习任务，调整学习算法的训练程度，

当训练不足时，模型拟合能力不够，训练数据的扰动不足以使得模型输出产生明显变化，此时bias主导了泛化误差，此时状态欠拟合
当训练充足时，模型拟合能力变强，训练数据的扰动会导致模型输出显著变化，此时var主导了泛化误差，此时状态过拟合