Pconv The Missing But Desirable Sparsity In Dnn Weight Pruning For Real Time Execution On Mobile Devices

https://arxiv.org/abs/1909.05073

Introduction

Background

DNN Model Compression

DNN模型压缩方法是去除原始模型中的冗余，从而减少计算图中的权重数目，加快推理速度。 压缩方法可以分为非结构化剪枝non-structured pruning和结构化剪枝structured pruning，产生的压缩模型对应为非规则的irregular和规则的regular。

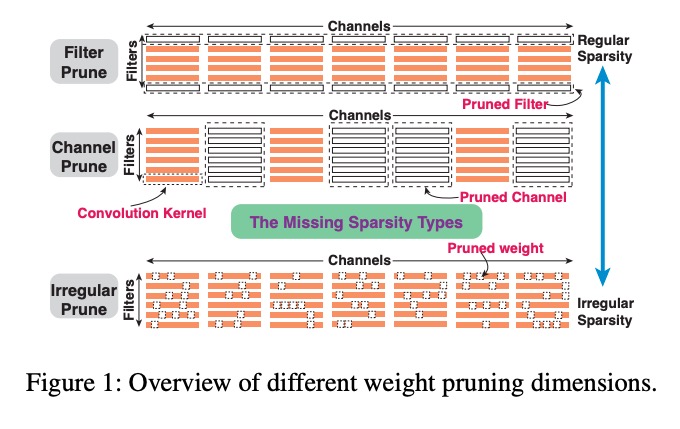
非结构化剪枝 Non-structured pruning

Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding Systematic Weight Pruning of DNNs using Alternating Direction Method of Multipliers ADMM-NN: An Algorithm-Hardware Co-Design Framework of DNNs Using Alternating Direction Method of Multipliers Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers NeST: A Neural Network Synthesis Tool Based on a Grow-and-Prune Paradigm 非结构化剪枝可以达到很高的剪枝率和保证一定的准确度，但是对于编译器和代码优化来说

• kernel里的非常规权重分布，带来非常重的控制开销，使得指令级别的并行度下降
• 多线程并发情况下，线程之间的工作量不平衡
• 内存访问效率低

结构化剪枝 structured pruning

Learning Structured Sparsity in Deep Neural Networks Channel Pruning for Accelerating Very Deep Neural Networks 可以避免非结构化剪枝带来的不平衡问题，但是无法避免性能下降

Patterns in Computer Vision

DNN Acceleration Frameworks on Mobile Platform

DeepCache: Principled Cache for Mobile Deep Vision DeepSense: A Unified Deep Learning Framework for Time-Series Mobile Sensing Data Processing 准确度和压缩率之间的tradeoff Sparse Convolutional Neural Networks 依赖新硬件 SCNN: An Accelerator for Compressed-sparse Convolutional Neural Networks

Motivations

本文受启发域以下三点

Achieving both high model accuracy and pruning regularity

在非结构化剪枝里，单核权重都可以被剪掉。这种方法有最大的灵活性flexibility，因此能够维持很高的正确性和压缩率。但是对硬件不友好。结构化剪枝生成的模型对硬件更友好，但是方法缺乏灵活性，造成正确性下降。 这里提出一个新的维度，基于pattern的稀疏性，可以同时兼顾以上优点。

Image enhancement inspired sparse convolution patterns

剪枝方法将剪枝看作是一种特殊的二分卷积操作，而没有开发相应的机会。我们发现稀疏矩阵pattern可以增强图像质量。

Compiler-assisted DNN inference framework

Theory of Sparse Convolution Patterns (SCP)

假设一张图片分辨率是$H\times W$，网络包含$L$层卷积，每层卷积$F_l$尺寸$H_l\times W_l$，输入通道是$C_l$，输出通道是$F_l$。 把剪枝过程看做，而是看做一个额外的二进制mask卷积核$P$，和原始的卷积核做逐点的乘法。卷积核$P$称为Sparse Convolution Pattern (SCP) 稀疏卷积pattern，尺寸和原始卷积核一致$[H_l, W_l, C_l, F_l]$，但是值是二进制0和1。由此，剪枝可以看做是在原始卷积核上应用了一次SCP。如下图所示，不同卷积核可以有不同SCP，但是SCP类型的总数是受限的。

为了进一步增加剪枝率，我们选择性地砍掉输入输出通道之间的连接，这等同于移除对应卷积核。这称为connectivity pruning 连通性剪枝。

The Convolution Operator

公式化表示 输入$f(x,y)$，权重$h(h,l)$，输出$g(x,y)$，卷积算法是 \(g(x,y) = \sum_{k,j}{f(x+k,y+l)h(k,l)}\) 或者写成 \(g(x,y) = \sum_{k,j}{f(k,l)h(x-k,y-l)}\) 简写成 \(g=f*h\)

Sparse Convolution Pattern (SCP) Design

高斯滤波器

一个二维的高斯滤波器$G$ \(G(x,y,\sigma)=\frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{w\sigma^2}}\) $x$和$y$是输入坐标，$\sigma$是高斯分布的标准差，通常高斯滤波器可以使图像更平滑。

拉普拉斯高斯滤波器

拉普拉斯算子是n维欧几里德空间中的一个二阶微分算子，二维函数$f(x,y)$的拉普拉斯算子是如下定义的二阶导数 \(\nabla^2f=\frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2}\) 拉普拉斯算子可以突出图像中强度发生快速变化的区域，因此常用在边缘检测任务当中。在进行Laplacian操作之前通常需要先用高斯平滑滤波器对图像进行平滑处理，以降低Laplacian操作对于噪声的敏感性。 用高斯滤波器做平滑，然后应用拉普拉斯操作，等效于在图片上用高斯拉普拉斯滤波器Laplacian of Gaussian (LoG) filter做卷积。 \(\nabla^2G(x,y,\sigma)=(\frac{x^2+y^2}{\sigma^4}-\frac{2}{\sigma^2})G(x,y,\sigma)\) LoG滤波器是一种带通滤波器，同时去除高频和低频噪声。

泰勒系数展开得到二阶导数近似

泰勒系数展开用于决定$3\times 3$的LoG滤波器的近似值。在离散的数字中，常常用差分来表示连续函数中的求导。 有限差分法求导 数字图像处理中，经常遇到求导的情况，但是我们的数字图像都是离散变量，因此无法直接对其求导，我们只能对其近似求导，所以此时我们可以采用有限差分求导对其近似求解 结论 \(f'(x_i)=(\frac{\partial f}{\partial x})_{x_i} \approx \frac{f(x_i+h)-f(x_i-h)}{2h} \\ f''(x_i)=(\frac{\partial^2 f}{\partial x^2})_{x_i} \approx \frac{f(x_i+h)+f(x_i-h)-2f(x_i)}{h^2} \\ \frac{\partial^2 f(x_i, y_i)}{\partial x\partial y} \approx \frac{1}{4h^2}[f(x_i+h, y_i+h)+f(x_i-h, y_i-h)-f(x_i+h, y_i-h)-f(x_i-h, y_i+h)]\) 推导证明 \(f'(x_i)=(\frac{\partial f}{\partial x})_{x_i} \approx \frac{f(x_i+h)-f(x_i-h)}{2h}\) 一元函数$f(x)$在任意点$x=x_i$泰勒级数展开公式为 \(f(x)=f(x_i)+f'(x_i)(x-x_i)+\frac{f''(x_i)}{2!}(x-x_i)^2+...+\frac{f^{(n)}(x_i)}{n!}(x-x_i)^n\) 求上式分别在$x=x_i+h$和$x=x_i-h$处的值 \(f(x_i+h)=f(x_i)+f'(x_i)(x_i+h-x_i)+\frac{f''(x_i)}{2!}(x_i+h-x_i)^2+... \\ =f(x_i)+f'(x_i)*h+\frac{f''(x_i)}{2}*h^2+... \\ f(x_i-h)=f(x_i)+f'(x_i)(x_i-h-x_i)+\frac{f''(x_i)}{2!}(x_i-h-x_i)^2+... \\ =f(x_i)-f'(x_i)*h+\frac{f''(x_i)}{2}*h^2+...\) 上面两个式子相减得到 \(f(x_i+h)-f(x_i-h) \approx f'(x_i)*2h\) 证明得到一元函数的一阶梯度近似表达 \(f'(x_i)=(\frac{\partial f}{\partial x})_{x_i} \approx \frac{f(x_i+h)-f(x_i-h)}{2h}\) 上面两个式子相加得到 \(f(x_i+h)+f(x_i-h) \approx 2f(x_i)+f''(x_i)h^2\) 证明得到一元函数的二阶梯度近似表达 \(f''(x_i) \approx \frac{f(x_i+h)+f(x_i-h)-2f(x_i)}{h^2}\) 二元函数$f(x,y)$在任意点$x=x_i y=y_i$泰勒级数展开公式为 \(f(x,y)=f(x_i, y_i)+(x-x_i)f'(x_i,y_i)+(y-y_i)f'(x_i,y_i)+\frac{1}{2!}(x-x_i)^2f''(x_i,y_i)+(x-x_i)(y-y_i)f''(x_i,y_i)+\frac{1}{2!}(y-y_i)^2f''(x_i,y_i)+...\) 求上式分别在$(x_i+h,y_i+h)$，$(x_i+h,y_i-h)$，$(x_i-h,y_i+h)$和$(x_i-h,y_i-h)$处的值 \(f(x_i+h,y_i+h)=f(x_i, y_i)+hf'(x_i,y_i)+hf'(x_i,y_i)+\frac{1}{2}h^2f''(x_i,y_i)+h^2f''(x_i,y_i)+\frac{1}{2}h^2f''(x_i,y_i)+... \\ =f(x_i, y_i)+2hf'(x_i,y_i)+2h^2f''(x_i,y_i)+... \\ f(x_i-h,y_i-h)=f(x_i, y_i)-hf'(x_i,y_i)-hf'(x_i,y_i)+\frac{1}{2}h^2f''(x_i,y_i)+h^2f''(x_i,y_i)+\frac{1}{2}h^2f''(x_i,y_i)+... \\ =f(x_i, y_i)-2hf'(x_i,y_i)+2h^2f''(x_i,y_i)+... \\ f(x_i+h,y_i-h)=f(x_i, y_i)+hf'(x_i,y_i)-hf'(x_i,y_i)+\frac{1}{2}h^2f''(x_i,y_i)-h^2f''(x_i,y_i)+\frac{1}{2}h^2f''(x_i,y_i)+... \\ =f(x_i, y_i)+... \\ f(x_i-h,y_i+h)=f(x_i, y_i)+hf'(x_i,y_i)-hf'(x_i,y_i)+\frac{1}{2}h^2f''(x_i,y_i)-h^2f''(x_i,y_i)+\frac{1}{2}h^2f''(x_i,y_i)+... \\ =f(x_i, y_i)+...\) 线性组合上列4个等式得到 \(f(x_i+h,y_i+h)+f(x_i-h,y_i-h)-f(x_i+h,y_i-h)-f(x_i-h,y_i+h) \approx \\ f(x_i, y_i)+2hf'(x_i,y_i)+2h^2f''(x_i,y_i)+f(x_i, y_i)-2hf'(x_i,y_i)+2h^2f''(x_i,y_i)-f(x_i, y_i)-f(x_i, y_i) \\ =4h^2f''(x_i,y_i)\) 证明得到二元函数的二阶梯度近似表达 \(f''(x_i,y_i) \approx \frac{1}{4h^2}[f(x_i+h,y_i+h)+f(x_i-h,y_i-h)-f(x_i+h,y_i-h)-f(x_i-h,y_i+h)]\)

应用以上结论，一元函数的二阶梯度近似表达 \(\nabla^2 G(x) \approx \frac{G(x+h)+G(x-h)-2G(x)}{h^2} \\ = \frac{1}\begin{bmatrix} 1 & -2 & 1 \end{bmatrix}*\begin{bmatrix} G(x-h) & G(x) & G(x+h) \end{bmatrix}^T\) 那么LoG滤波器的一维近似表达为$\begin{bmatrix} 1 & -2 & 1 \end{bmatrix}$ 进一步得到，LoG滤波器的二维近似是$\begin{bmatrix} 1 & -2 & 1 \end{bmatrix}$和$\begin{bmatrix} 1 \ -2 \ 1 \end{bmatrix}$做卷积，得到第一个LoG滤波器的二元近似 \(LoG_{filter} = \begin{bmatrix} -1 & 2 & -1 \\ 2 & -4 & 2 \\ -1 & 2 & -1 \end{bmatrix}\) 根据多元函数导数特性 \(\nabla^2 G(x,y) =\frac{\partial^2 G}{\partial x^2}+\frac{\partial^2 G}{\partial y^2} \\ =\nabla^2 G_x(x,y)+\nabla^2 G_y(x,y) \\ =(\begin{bmatrix} 1 & -2 & 1 \end{bmatrix} + \begin{bmatrix} 1 \\ -2 \\ 1 \end{bmatrix})G(x,y) \\ =\begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{bmatrix}G(x,y)\) 得到第一个LoG滤波器的二维近似 \(LoG_{filter} = \begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{bmatrix}\)

根据中心极限定理central limit theorem，两个高斯函数的卷积仍然是高斯函数，新的高斯函数的方差是两个原始高斯函数方差之和。因此，我们将上面两个LoG滤波器的二维近似做卷积，得到增强拉普拉斯高斯滤波器ELoG。 \(LoG_{filter} = \begin{bmatrix} 0 & 1 & 0 \\ 1 & 8 & 1 \\ 0 & 1 & 0 \end{bmatrix}\) The Power of Interpolation: Understanding the Effectiveness of SGD in Modern Over-parametrized Learning中证明了，多层DNN中插值仍然会收敛，我们利用这一点进一步做近似。在ELoG滤波器中，以$(1-p)$的概率将1变为0。因为我们均匀地将SCP卷积进$n$个卷积核，那么随机mask操作可以看做是SCP插值。在连续的概率空间内，卷积的SCP插值函数是特定的概率密度函数，那么SCP插值的效果就是$n$层插值的概率期望之和。如下如所示

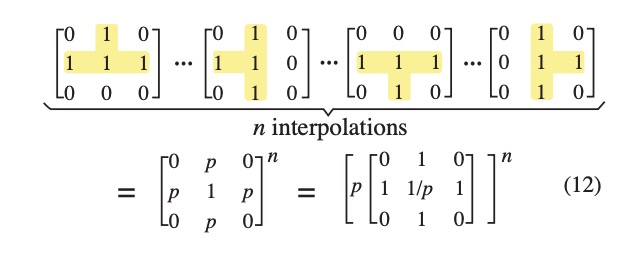
上图中假设所有卷积核都是归一化的，因此可以将$p$提取出来。 上图中展示了4个SCP。